三维无限深势阱¶
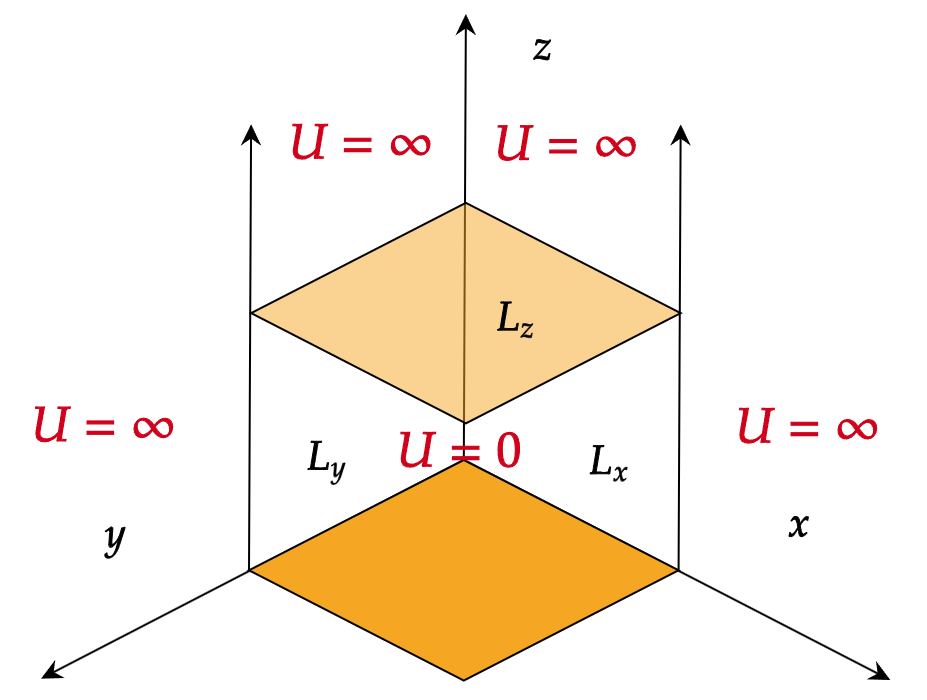
一个粒子束缚于三维无限深方形阱内,阱宽在 \(x\)、\(y\)、\(z\) 方向,分别为 \(L_{x}\)、\(L_{y}\)、\(L_{z}\)。
阱内位势为 0 ,阱外位势为无限大。
粒子只能移动于束缚的方向(\(x\)、\(y\)、\(z\) 方向)。
设三维无限深势阱的势能分布如下:
\[U(x,y,z)=\left\{\begin{array}{ll}0 & if~~0<x<L_x~~and~~0<y<L_y~~and~~0<y<L_z \\\infty & otherwise \end{array}\right.\]
在这三维的问题里,粒子束缚于一个三维势阱内。
在阱外,设波函数为 \(\psi_e\),定态薛定谔方程为:
\[\displaystyle-\frac{\hbar}{2 m}(\frac{\mathrm{d}^{2} \psi_{\mathrm{e}}}{\mathrm{d} x^{2}}+\frac{\mathrm{d}^{2} \psi_{\mathrm{e}}}{\mathrm{d} y^{2}}+\frac{\mathrm{d}^{2} \psi_{\mathrm{e}}}{\mathrm{d} z^{2}})+(E-U(x,y,z)) \psi_{\mathrm{e}}=0\]
由于在阱外,\(U(x,y,z)\rightarrow \infty\),对于 \(E\) 为有限值的粒子,要使上述方程成立,唯有 \(\psi_e=0\)。
在阱内,设波函数为 \(\psi_i\),定态薛定谔方程为:
\[\displaystyle-\frac{\hbar^{2}}{2 m}\left(\frac{\partial^{2} \psi_i}{\partial x^{2}}+\frac{\partial^{2} \psi_i}{\partial y^{2}}+\frac{\mathrm{d}^{2} \psi_{\mathrm{e}}}{\mathrm{d} z^{2}}\right)=E \psi_i\]
使用分立变量法,我们假设 \(\psi_i(x, y,z)\) 是三个不相关的函数 \(X(x)\)、\(Y(y)\)、\(Z(z)\) 的乘积:
\[\psi_{i}(x, y,z)=X(x) Y(y)Z(z)\]
将上式带入阱内的薛定谔方程:
\[\displaystyle-\frac{\hbar^{2}}{2 m}\left(YZ \frac{\partial^{2} X}{\partial x^{2}}+XZ \frac{\partial^{2} Y}{\partial y^{2}}+XY \frac{\partial^{2} Z}{\partial z^{2}}\right)=E XYZ\]
将方程两边都除以 \(XYZ\),我们可以得到:
\[\displaystyle-\frac{\hbar^{2}}{2 m}\left(\frac{X^{\prime \prime}}{X}+\frac{Y^{\prime \prime}}{Y}+\frac{Z^{\prime \prime}}{Z}\right)=E\]
由于 \(\displaystyle\frac{X^{\prime \prime}}{X}\)、\(\displaystyle\frac{Y^{\prime \prime}}{Y}\)、\(\displaystyle\frac{Z^{\prime \prime}}{Z}\)分别只和 \(x\)、\(y\)、\(z\) 有关,则上式右边的能量可以写成 \(E_{x}+E_{y}+E_{z}=E\)。
我们可以将上式分离,分离的三个式子分别等于对应的常数:
\[
\begin{array}{c}\displaystyle-\frac{\hbar^{2}}{2 m} \frac{X^{\prime \prime}}{X}=E_{x}\\\displaystyle-\frac{\hbar^{2}}{2 m} \frac{Y^{\prime \prime}}{Y}=E_{y}\\\displaystyle-\frac{\hbar^{2}}{2 m} \frac{Z^{\prime \prime}}{Z}=E_{z}\end{array}
\]
上述两式也可以写成:
\[
\begin{array}{c}\displaystyle-\frac{\hbar^{2}}{2 m} \frac{d^{2} X}{d x^{2}}=E_{x} X\\\displaystyle-\frac{\hbar^{2}}{2 m} \frac{d^{2} Y}{d y^{2}}=E_{y} Y\\\displaystyle-\frac{\hbar^{2}}{2 m} \frac{d^{2} Z}{d z^{2}}=E_{z} Z\end{array}
\]
根据之前的“一维无限深势阱”的文章:
上述三式的解可以写成:
\[
\begin{array}{c}\displaystyle X_{n_{x}}(x)=\sqrt{\frac{2}{L_{x}}} \sin \left(\frac{n_{x} \pi x}{L_{x}}\right),\quad n_{x}=1,2,3, \cdots\\\displaystyle E_{n_x}=\frac{n_x^{2} \pi^{2} \hbar^{2}}{2 m L_x^{2}}\\\displaystyle Y_{n_{y}}(y)=\sqrt{\frac{2}{L_{y}}} \sin \left(\frac{n_{y} \pi y}{L_{y}}\right),\quad n_{y}=1,2,3, \cdots\\\displaystyle E_{n_y}=\frac{n_y^{2} \pi^{2} \hbar^{2}}{2 m L_y^{2}}\\\displaystyle Y_{n_{z}}(z)=\sqrt{\frac{2}{L_{z}}} \sin \left(\frac{n_{z} \pi z}{L_{z}}\right),\quad n_{z}=1,2,3, \cdots\\\displaystyle E_{n_z}=\frac{n_z^{2} \pi^{2} \hbar^{2}}{2 m L_z^{2}}\end{array}
\]
根据式子 \(\psi_{i}(x, y,z)=X(x) Y(y)Z(z)\),我们可以得到:
\[
\begin{array}{c}\displaystyle\psi_{n_{x}, n_{y},n_{z}}(x,y,z)=\sqrt{\frac{8}{L_{x} L_{y}L_{z}}} \sin \left(\frac{n_{x} \pi x}{L_{x}}\right) \sin \left(\frac{n_{y} \pi y}{L_{y}}\right)\sin \left(\frac{n_{z} \pi z}{L_{z}}\right)\\\displaystyle E_{n_x,n_y,n_z}=E_{n_x}+E_{n_y}+E_{n_z}=\frac{ \pi^{2} \hbar^{2}}{2 m}\left[\left(\frac{n_{x}}{L_{x}}\right)^{2}+\left(\frac{n_{y}}{L_{y}}\right)^{2}+\left(\frac{n_{z}}{L_{z}}\right)^{2}\right]\\n_{x}=1,2,3, \cdots\\n_{y}=1,2,3, \cdots\\n_{z}=1,2,3, \cdots\end{array}
\]