倒格子（Reciprocal Lattice）¶

一个物理问题，既可以在正空间（坐标空间）描写，也可以在倒空间（动量）描写。

对于一个问题，我们可以选择不同的描写方法。合适的描写方法可以帮我们简化问题。

坐标空间中用格矢（ $\mathbf{R}_{l}$ ）描写晶体平移周期性。

势能、电荷密度等满足叠加原理的物理量：$\displaystyle F(\mathbf{r})=\sum_l f\left(\mathbf{r}-\mathbf{R}_{l}\right)$

如果晶体具有平移周期性，则格矢满足条件：$\mathbf{R}_{l}=\mathbf{R}_{m}+\mathbf{R}_{n}$

满足叠加原理的物理量可以写作格矢 $\mathbf{R}_{l}$ 的周期函数：$F\left(\mathbf{r}+\mathbf{R}_{l}\right)=F(\mathbf{r})$

对物理量 $F(\mathbf{r})$ 作傅里叶展开：$\displaystyle F(\mathbf{r})=\sum_{h} F_{\mathbf{K}_{h}} e^{-i\mathbf{K}_{h} \cdot \mathbf{r}}$

$F_{\mathbf{K}_{h}}$被称为傅里叶系数。

将两边乘以共轭因子 $\displaystyle e^{-i\mathbf{K}_{h} \cdot \mathbf{r}}$ 后并积分，我们可以得到：

\[\displaystyle\frac{1}{V} \int F(\mathbf{r}) e^{-\mathbf{K}_{h} \cdot\mathbf{r}} d \mathbf{r}=\sum_{h'} F_{\mathbf{K}_{h'}} \frac{1}{V} \int e^{i\left(\mathbf{K}_{h'}-\mathbf{K}_{h}\right\rangle \mathbf{\cdot r}} d \mathbf{r}\]

当且仅当 $\mathbf{K}_{h'}=\mathbf{K}_{h}$ 的时候，这个积分不为零，且等于 $V$ 。

\[\displaystyle\frac{1}{V} \int F(\mathbf{r}) e^{-\mathbf{K}_{h} \cdot\mathbf{r}} d \mathbf{r}=F_{\mathbf{K}_h}\frac{1}{V}V=F_{\mathbf{K}_h}\]

因为 $F(\mathbf{r})$ 具有周期性，所以傅里叶系数对应的公式中加上格矢，傅里叶系数 $\mathbf{R}_{l}$ 是不变的：

\[\displaystyle F_{\mathbf{K}_{h}}=\frac{1}{V} \int F(\mathbf{r}) e^{-\mathbf{K_h}\cdot \mathbf{r}} d \mathbf{r}=\frac{1}{V} \int F\left(\mathbf{r}+\mathbf{R}_{l}\right) e^{-\mathbf{K}_{h}\cdot \mathbf{r}} d \mathbf{r}\]

做变量替换 $\mathbf{r}^{\prime}=\mathbf{r}+\mathbf{R}_{l}$ ，傅里叶系数可以变换为：

\[\begin{array}{ll} F_{\mathbf{K}_{h}}&\displaystyle=\frac{1}{V} \int F\left(\mathbf{r}^{\prime}\right) e^{-i\left(\mathbf{K}_{h} \cdot \mathbf{r}^{\prime}-\mathbf{K}_{h} \cdot \mathbf{R}_{l}\right)} d \mathbf{r}^{\prime} \\&\displaystyle=\left[\frac{1}{V} \int F\left(\mathbf{r}^{\prime}\right) e^{-i \mathbf{K}_{h}\cdot \mathbf{r}^{\prime}} d \mathbf{r}^{\prime}\right] e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}\\&\displaystyle=F_{\mathbf{K}_{h}} e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}} \\\end{array}\]

上式可以写成： $\displaystyle F_{\mathbf{K}_{h}}\left(1-e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}\right)=0$

显然$\displaystyle F_{\mathbf{K}_{h}} \neq 0$，所以我们可以知道，如果晶体具有周期性，则一定满足公式：$e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}=1$

其中$\mathbf{K}_{h} \bullet \mathbf{R}_{l}=2 \pi m$，$m$是整数。

格点如何进行傅里叶变换？¶

数学上如何用一个函数来描写格点？

在数学上，我们用$\delta$函数来描写晶体中的格点。

将一个晶体中所有格点对应的$\delta$函数加起来，我们可以得到：

\[\displaystyle\rho(\mathbf{r})=\sum_{\mathbf{R}_{l}} \delta\left(\mathbf{r}-\mathbf{R}_{l}\right)\]

这是周期函数，因此可对其进行傅里叶变换：

\[\displaystyle\rho_{\mathbf{k}}=\int \rho(\mathbf{r}) e^{-i \mathbf{k} \cdot \mathbf{r}} d \mathbf{r}=\sum_{\mathbf{R}_{l}} \int \delta\left(\mathbf{r}-\mathbf{R}_{l}\right) e^{-i \mathbf{k} \cdot \mathbf{r}} d \mathbf{r}=\sum_{\mathbf{R}_{l}} e^{-\mathbf{k} \cdot \mathbf{R}_{l}}\]

格点满足平移周期性，则 $\mathbf{K}_{h}$ 满足：$\mathbf{K}_{h} \bullet \mathbf{R}_{l}=2 \pi m$

那么乘上不变因子 $e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}=1$ ，我们可以得到：$\displaystyle\rho_{\mathbf{k}}=\sum_{\mathbf{R}_{l}} e^{-i\left(\mathbf{k}-\mathbf{K}_{h}\right)\cdot \mathbf{R}_l}$

利用泊松求和公式 $\displaystyle\sum_{n=-\infty}^{\infty} \delta\left(t-n T_{0}\right)=\frac{1}{T_{0}} \sum_{n=-\infty}^{\infty} e^{j 2 \pi n \frac{1}{T_{0}} t}$ ，我们可以得到：

\[\displaystyle\rho_{\mathbf{k}}=\sum_{\mathbf{R}_{l}} e^{i\left(\mathbf{k}- \mathbf{K}_{h}\right) \cdot \mathbf{R_l}}=\sum_{\mathbf{K}_{h}} \delta\left(\mathbf{k}-\mathbf{K}_{h}\right)\]

即当矢量 $\mathbf{K}_{h}$ 与 $\mathbf{R}_{l}$ 的乘积是 $2\pi$ 的整数倍的时候，坐标空间中以 $\mathbf{R}_{l}$ 为中心的 $\delta$ 函数在傅里叶变换后，变为在动量空间中以 $\mathbf{K}_{h}$ 为中心的 $\delta$ 函数！

我们可以发现：坐标空间几何点的傅里叶变换也是几何点！

$\mathbf{K}_{h}$ 与 $\mathbf{R}_{l}$ 的关系定义了倒空间矢量，$\mathbf{K}_{h}$ 的量纲为 $\mathbf{R}_{l}$ 量纲的倒数。

倒格子¶

定义

对布拉菲格子（正格子）中所有的格式 $\mathbf{R}_{l}$ ，有一系列动量空间矢量 $\mathbf{K}_{h}$ ，满足 $\displaystyle e^{i \mathbf{K}_{h} \cdot \mathbf{R}_{l}}=1$ 和 $\mathbf{K}_{h} \bullet \mathbf{R}_{l}=2 \pi m$（ $m$ 是整数）的全部端点 $\mathbf{K}_{h}$ 的集合，构成布拉菲格子的倒格子，这些点称为倒格点， $\mathbf{K}_{h}$ 称为倒格矢。

等价关系：知道 $\mathbf{K}_{h}$ ，就知道 $\mathbf{R}_{l}$，反过来也一样。

因为它们满足傅里叶变换关系，所以倒空间也称为傅里叶空间。

倒格子基矢¶

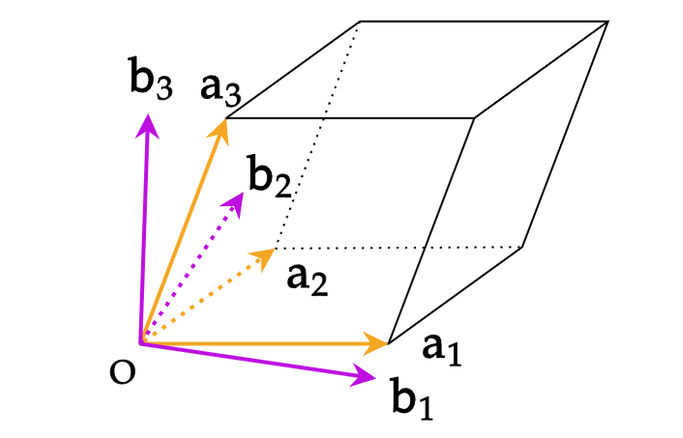
布拉菲格子（正格子）的基矢为：$\mathbf{R}_{l}=l_{1} \mathbf{a}_{1}+l_{2} \mathbf{a}_{2}+l_{3} \mathbf{a}_{3}$

将上式带入关系：$\mathbf{K}_{h} \cdot \mathbf{R}_{l}=l_{l} \mathbf{K}_{h} \cdot \mathbf{a}_{1}+l_{2} \mathbf{K}_{h} \cdot \mathbf{a}_{2}+l_{3} \mathbf{K}_{h} \cdot \mathbf{a}_{3}=2 \pi m$

如果选择一组矢量 $\bf b$，使其满足关系：$\mathbf{b}_{i} \cdot \mathbf{a}_{j}=2 \pi \delta_{i j}$

那么矢量 $\mathbf{K}_{h}$ 就可由 $\bf b$ 组成： $\mathbf{K}_{h}=h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{3} \mathbf{b}_{3}$

这样就定义了倒格子基矢，因为它可以满足正、倒格矢之间的 $\mathbf{K}_{h} \bullet \mathbf{R}_{l}=2 \pi m$ 的关系。

因为形式上与正格矢一样，所以 $\mathbf{K}_{h}$ 也具有平移对称性（周期性）。

我们可以用基矢和整数表示平移对称性。

$\mathbf{K}_{h}$定义了倒空间的布拉菲格子，$\mathbf{b}_i$ 就是倒格子基矢。

$\mathbf{b}_{i} \cdot \mathbf{a}_{j}=2 \pi \delta_{i j}$表示正、倒格矢的基矢之间是正交关系！即 $\bf b_1$ 与 $\bf a_2$ 和 $\bf a_3$ 正交！

看 $\bf a_2$ 和 $\bf a_3$ 确定的平面，即 $\bf a_2\times a_3$ 矢量垂直于该平面。

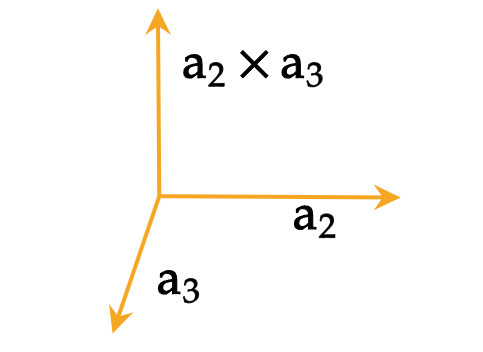
因为 $\bf b_1$ 与 $\bf a_2$ 和 $\bf a_3$ 分别正交，所以矢量 $\bf b_1$ 与矢量 $\bf a_2\times a_3$ 平行！

因此，可设 $\mathbf{b}_{1}=\eta\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)$ 。

我们可以利用正交关系确定 $\eta$ ：

\[ \begin{align*} \mathbf{a}_{1} \cdot \mathbf{b}_{1} &= \eta \mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right) = 2 \pi \\ \eta &= \frac{2 \pi}{\mathbf{a_{1}} \cdot\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)} = \frac{2 \pi}{\Omega} \\ \mathbf{b}_{1} &= \frac{2 \pi}{\Omega}\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right) \\ \Omega &= \left|\mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)\right| \end{align*} \]

同理，我们可以求出倒空间所有的基矢：

\[\begin{array}{l}\displaystyle\rm\mathbf{b}_{1}=2 \pi \frac{\mathbf{a}_{2} \times \mathbf{a}_{3}}{\mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)} \\\displaystyle\rm\mathbf{b}_{2}=2 \pi \frac{\mathbf{a}_{3} \times \mathbf{a}_{1}}{\mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)} \\\displaystyle\rm\mathbf{b}_{3}=2 \pi \frac{\mathbf{a}_{1} \times \mathbf{a}_{2}}{\mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)}\end{array}\]

有些教科书也将这个关系作为倒格子基矢的定义，即由这三个矢量可以定义倒格矢，倒格矢给出的端点集合构成倒格子。

正格子和倒格子互为倒正，即正格子也可以看作倒格子的倒格子。

\[\begin{array}{l}\displaystyle\mathbf{b}_{1}=2 \pi \frac{\mathbf{a}_{2} \times \mathbf{a}_{3}}{\mathbf{a}_{1} \cdot\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)} \\\displaystyle\mathbf{b}_{2}=2 \pi \frac{\mathbf{a}_{3} \times \mathbf{a}_{1}}{\mathbf{a}_{1} \cdot\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)} \\\displaystyle\mathbf{b}_{3}=2 \pi \frac{\mathbf{a}_{1} \times \mathbf{a}_{2}}{\mathbf{a}_{1} \cdot\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)}\end{array}\Leftrightarrow \begin{array}{l}\displaystyle\mathbf{a}_{1}=2 \pi \frac{\mathbf{b}_{2} \times \mathbf{b}_{3}}{\mathbf{b}_{1} \cdot\left(\mathbf{b}_{2} \times \mathbf{b}_{3}\right)} \\\displaystyle\mathbf{a}_{2}=2 \pi \frac{\mathbf{b}_{3} \times \mathbf{b}_{1}}{\mathbf{b}_{1} \cdot\left(\mathbf{b}_{2} \times \mathbf{b}_{3}\right)} \\\displaystyle\mathbf{a}_{3}=2 \pi \frac{\mathbf{b}_{1} \times \mathbf{b}_{2}}{\mathbf{b}_{1} \cdot\left(\mathbf{b}_{2} \times \mathbf{b}_{3}\right)}\end{array}\]

倒格矢： $\mathbf{K}_{h}=h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{3} \mathbf{b}_{3}$

满足平移对称性：$\mathbf{K}_{h}=\mathbf{K}_{h^{\prime}}+\mathbf{K}_{h^{\prime \prime}}$

在量纲上，倒格子原胞体积是正格子原胞体积的倒数：

\[\displaystyle\Omega^{*}=\left|\mathbf{b}_{1} \cdot\left(\mathbf{b}_{2} \times \mathbf{b}_{3}\right)\right|=\frac{(2 \pi)^{3}}{\Omega}\]

二维倒格子¶

我们将其中一个维度看成是单位矢量：$\mathbf{a}_{3}=\hat{\mathbf{k}}$

\[\begin{array}{l}\displaystyle\rm\mathbf{b}_{1}=2 \pi \frac{\mathbf{a}_{2} \times \hat{\mathbf{k}}}{\hat{\mathbf{k}} \cdot\left(\mathbf{a}_{1} \times \mathbf{a}_{2}\right)} \\\displaystyle\rm\mathbf{b}_{2}=2 \pi \frac{\hat{\mathbf{k}} \times \mathbf{a}_{1}}{\hat{\mathbf{k}} \cdot\left(\mathbf{a}_{1} \times \mathbf{a}_{2}\right)}\end{array}\]

\[\begin{array}{l} \mathbf{a}_{1}=a \hat{\mathbf{i}} \\ \mathbf{a}_{2}=b \hat{\mathbf{j}}\end{array}\Rightarrow\begin{array}{l}\displaystyle\mathbf{b}_{1}=\frac{2 \pi}{a} \hat{\mathbf{i}} \\\displaystyle\mathbf{b}_{2}=\frac{2 \pi}{b} \hat{\mathbf{j}}\end{array}\]

倒格子与布拉菲格子的几何关系¶

正、倒格子描述不同空间的晶体对称性。

正、倒格子对应的几何关系：

$\mathbf{K}_{h}=h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{3} \mathbf{b}_{3}$ 与晶面 $(h_1h_2h_3)$ 正交。

倒格式的方向就是晶面的法向。

注：不是密勒指数 $(hkl)$ ，而是晶面指数 $(h_1h_2h_3)$ 。

该晶面族最靠近原点晶面的截距分别为：$\displaystyle\frac{a_1}{h_1}$，$\displaystyle\frac{a_2}{h_2}$，$\displaystyle\frac{a_3}{h_3}$；

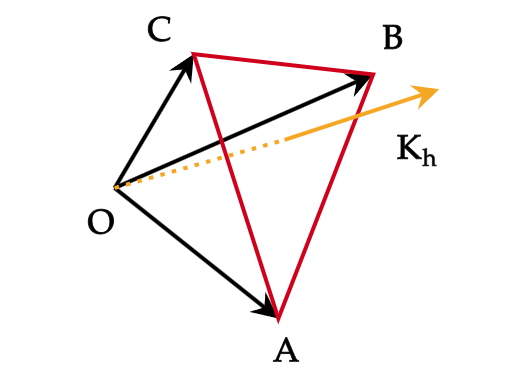
证明：

\[ \begin{align*} \mathbf{C A} &= \mathbf{O A}-\mathbf{O C}=\frac{\mathbf{a}_{1}}{h_{1}}-\frac{\mathbf{a}_{3}}{h_{3}} \\ \mathbf{CB} &= \mathbf{OB}-\mathbf{OC}=\frac{\mathbf{a}_{2}}{h_{2}}-\frac{\mathbf{a}_{3}}{h_{3}} \\ \mathbf{K}_{h} \cdot \mathbf{C A} &= \left(h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{1} \mathbf{b}_{3}\right) \cdot\left(\frac{\mathbf{a_1}}{h_{1}}-\frac{\mathbf{a}_{3}}{h_{3}}\right)=0 \\ \mathbf{K}_{h} \cdot \mathbf{C B} &= \left(h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{1} \mathbf{b}_{3}\right) \cdot\left(\frac{\mathbf{a}_{2}}{h_{2}}-\frac{\mathbf{a}_{3}}{h_{3}}\right)=0 \end{align*} \]

所以我们可以证得：$\mathbf{K}_{h}$垂直于平面 $\bf ABC$ ，即 $\mathbf{K}_{h}$ 与晶面 $(h_1h_2h_3)$ 正交。

倒格矢的长度与面间距¶

设晶面 $(h_1h_2h_3)$ 的面间距为 $d$ ；

则最靠近原点的晶面到原点的距离即 $\mathbf{OA}$ 在 $\mathbf{K}_{h}$ 上的投影：

\[\begin{aligned}\displaystyle d &\displaystyle =\frac{\mathbf{a}_{1}}{h_{1}} \cdot \frac{\mathbf{K}_{h}}{\left|\mathbf{K}_{h}\right|} \\\displaystyle & =\frac{\mathbf{a}_{1} \cdot\left(h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{3} \mathbf{b}_{3}\right)}{h_{1}\left|h_{1} \mathbf{b}_{1}+h_{2} \mathbf{b}_{2}+h_{3} \mathbf{b}_{3}\right|} \\\displaystyle & =\frac{2 \pi}{\left|\mathbf{K}_{h}\right|}\end{aligned}\]

\[\displaystyle\mid\mathbf{K}_{h}\mid=\frac{2 \pi}{d_{h}}\]

\[\displaystyle\mathbf{K}_{h}=\frac{2 \pi}{d_h} \hat{\mathbf{n}}_{h}\]

注：面间距是与晶面指数而不是密勒指数相关。

自原点 $\bf O$ 引晶面族法线 $\bf N$ ，截取 $\bf P$ 使 $\displaystyle \mathbf{OP}=\frac{2\pi}{d}$ 。

$\bf P$点即倒格点，沿 $\bf N$ 平移 $\bf OP$ ，形成格子，即倒格子。

这样我们可以把晶面和倒格点相互联系起来，即将衍射极大与晶面相联系起来。

倒格子与基矢与正格子基矢的关系¶

正格子基矢组成 $\mathbf{a}_{1} \mathbf{a}_{2}, \mathbf{a}_{2} \mathbf{a}_{3}, \mathbf{a}_{3} \mathbf{a}_{1}$ 坐标面，各有对应晶面，面间距分别是 $ d_{1}, d_{2}, d_{3}$ 。

可作 $\bf OP$ 垂直于 $\mathbf{a}_{1} \mathbf{a}_{2}$ 晶面，取长度为 $\displaystyle b_3=\frac{2\pi}{d_3}$ 。同理，得 $ b_2,b_3$ 。

例子¶

简单立方（Simple Cubic）¶

注：简单立方格子的倒格子是简单立方格子。

体心立方（Body Centered Cubic）¶

注：体心立方格子的倒格子是面心立方格子。

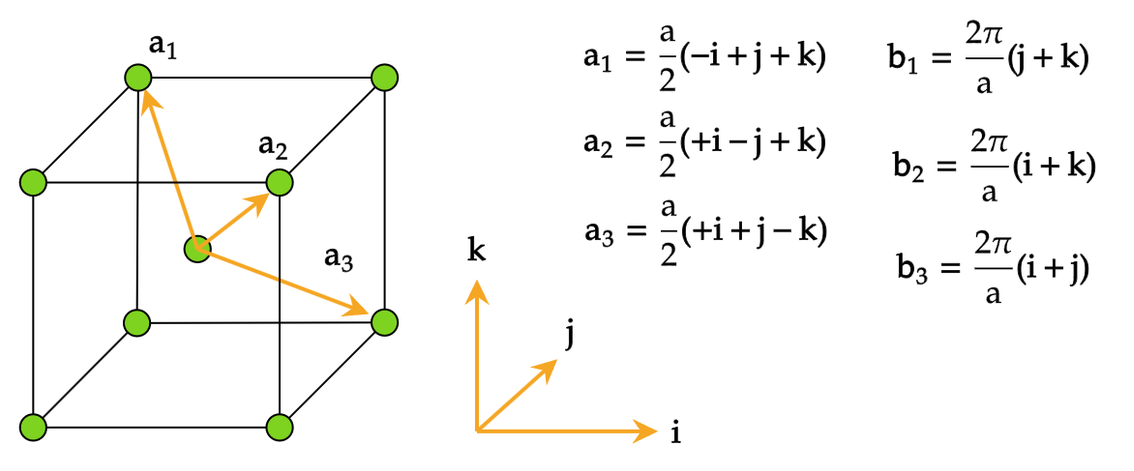
面心立方（Face Centered Cubic）¶

注：面心立方格子的倒格子是体心立方格子。

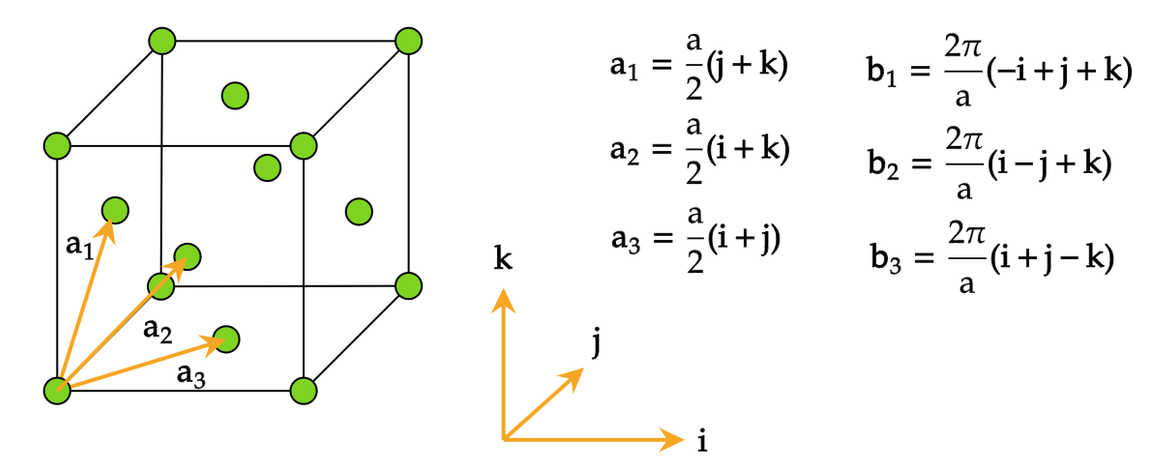
简单六角（Simple Hexagon）¶

注：简单六角格子的倒格子是简单六角格子。

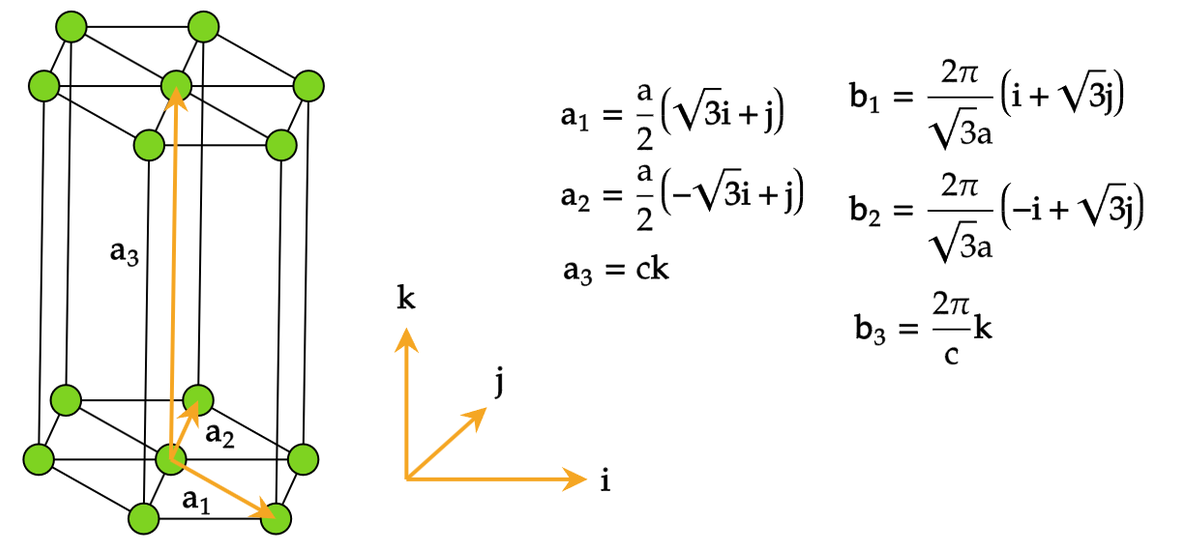
例题¶

面心立方下述晶面的面间距是多少？

解：

首先，上述晶面的密勒指数是：$\rm (100)$

以原胞基矢为单位，三个方向上的截距为：$\infty, 1,1$

截距的倒数互质的最小整数为（晶面指数）：$\rm (011)$

根据晶面间距公式 $\displaystyle d=\frac{2 \pi}{\left|\mathbf{K}_{h}\right|}$ 和上述面心立方的倒格子基矢，我们可以得到面心立方格子的晶面间距为：

\[\displaystyle d=\frac{2 \pi}{\mathbf{K}_{h}}=\frac{2 \pi}{\mathbf{b}_{2}+\mathbf{b}_{3}}=\frac{2 \pi}{\displaystyle\frac{2 \pi}{a}[(+\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}})+(+\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}})]}=\frac{a}{2}\]

问题¶

问题1：固体物理中为什么要引入倒空间（动量空间）的概念？

在固体物理中，引入倒空间（也称为动量空间或 $\bf k$ 空间）的概念是非常重要的，原因有几方面：

简化问题：倒空间是通过傅里叶变换从实空间（物理空间，即我们通常观察到的空间）转换而来的。在处理固体中的电子行为和晶体结构时，使用倒空间可以简化问题。例如，晶体的周期性边界条件在倒空间中更容易处理，因为晶格的周期性在倒空间中表现为离散的点，这使得分析和计算晶体的电子结构和振动模式变得更加直观和简单。
布拉格衍射：倒空间在分析晶体的 X 射线衍射中尤其有用。布拉格定律描述了晶体中原子平面对 X 射线的衍射，这可以在倒空间中非常自然地表示。在倒空间中，晶体的布拉格平面对应于特定的点，这些点的位置与晶体结构的周期性直接相关。通过研究这些点，科学家可以直观地理解和分析晶体的结构特征。
电子能带结构：在固体物理中，电子的行为可以通过其能带结构来描述，而能带结构在倒空间中表示更为直接。倒空间中的每个点对应于一个特定的波矢（动量），这允许直接计算和表示电子的能量分布和禁带结构。这对于理解和预测材料的电子性质至关重要，如导电性、绝缘性和半导体性质。
波动性质和周期性：固体中的电子、声子（晶格振动的量子）和其他准粒子的行为通常具有波动性质，这些波动性质在倒空间中更容易分析。例如，声子的色散关系（即声子能量与其动量的关系）通常在倒空间中给出，这有助于理解固体中热力学和机械性质的基础。
Bloch 定理：Bloch 定理是固体物理中的一个基本定理，它表明在周期性势场中的电子波函数可以表示为平面波和周期性函数的乘积。这一定理的自然语言就是倒空间，因为它直接关联了电子的波矢（动量）和晶体的周期性。

总之，倒空间的引入为理解和分析固体中的复杂现象提供了一种强有力的工具，使得许多原本在实空间中难以处理的问题变得更加可解和直观。

问题2：给定的正格子是否只有唯一的倒格子与之对应？

在晶体物理中，给定的正格子确实只有一个唯一对应的倒格子。正格子是用来描述晶体中原子排列的三维网格，而倒格子则是用来描述晶体的波动性质，如电子波或 X 射线的衍射模式。

倒格子的构造是基于正格子的，其基矢量与正格子的基矢量之间存在特定的数学关系。这种关系确保了每一个正格子只对应一个唯一的倒格子。倒格子的基矢量是正格子基矢量的函数，通过特定的数学变换得到，这种变换包括计算正格子基矢量的互相垂直的向量并进行归一化处理。

倒格子的概念在分析和理解晶体内部的波动性质（如电子的行为、光波和声波的传播等）方面非常重要，因为它提供了一个方便的数学框架来研究这些性质。这种唯一对应关系保证了晶体的物理性质可以通过研究其倒格子得到全面的理解。

问题3：给定的正格子基矢是否只有唯一的倒格子基矢与之对应？

在固体物理中，正格子与倒格子的概念是用于描述晶体结构的重要工具。正格子定义了晶体中原子或分子的周期性排列，而倒格子则是用来描述波动性质，如电子波和声子波在晶体中的传播。

给定的正格子基矢确实只有一组唯一的倒格子基矢与之对应。倒格子基矢是通过正格子基矢通过一组特定的数学变换得到的，这个变换基于正格子基矢构建一个与原晶体具有相同对称性但在倒空间中的格子。倒格子的基矢与正格子的基矢满足以下关系：

如果正格子的基矢是 $\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}$ ，那么对应的倒格子基矢 $\mathbf{b}_{1}, \mathbf{b}_{2}, \mathbf{b}_{3}$可以通过下面的公式计算得到：

\[\begin{array}{l}\displaystyle\rm\mathbf{b}_{1}=2 \pi \frac{\mathbf{a}_{2} \times \mathbf{a}_{3}}{\mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)} \\\displaystyle\rm\mathbf{b}_{2}=2 \pi \frac{\mathbf{a}_{3} \times \mathbf{a}_{1}}{\mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)} \\\displaystyle\rm\mathbf{b}_{3}=2 \pi \frac{\mathbf{a}_{1} \times \mathbf{a}_{2}}{\mathbf{a}_{1} \bullet\left(\mathbf{a}_{2} \times \mathbf{a}_{3}\right)}\end{array}\]

这些公式确保了倒格子基矢与正格子基矢之间的正交性和体积关系，从而使得倒格子基矢唯一对应于一组给定的正格子基矢。这种唯一性是晶体物理和固体物理研究中的基本性质，是分析晶体中电子行为和声子散射过程的基础。

问题4：正格矢 $\mathbf{R}_l$ 是否只有唯一的倒格式 $\mathbf{K}_h$ 与之对应？

不是的，对于一个给定的正格矢 $\mathbf{R}_l$ ，并不存在唯一的倒格矢 $\mathbf{K}_h$ 与之对应。这是因为正格矢和倒格矢定义在不同的空间中，它们遵循的是一种正交性关系，而非一一对应的关系。

正格矢 $\mathbf{R}_l$ 描述的是晶体直接空间（或称为实空间）中的周期性结构，它表示晶体中原子或分子重复出现的位置。倒格矢 $\mathbf{K}_h$ 则定义在倒空间中，用来描述波动性质，如电子波函数的相位变化。正格矢和倒格矢之间的关系通常通过布拉菲定理（Bragg's law）在物理上得到体现，而数学上它们遵循的是：

\[e^{i\mathbf{K}_h \cdot \mathbf{R}_l} = 1\]

这个方程表明，当倒格矢 $\mathbf{K}_h$ 与某个正格矢 $\mathbf{R}_l$ 的点积满足 $2\pi$ 的整数倍时，波函数的相位变化为 $2\pi m$（$m$是整数），意味着波函数回到了其原始值。这说明对于给定的 $\mathbf{R}_l$ ，存在多个 $\mathbf{K}_h$ 可以满足上述条件，因为倒空间中有无限多个点可以与 $\mathbf{R}_l$ 形成这样的点积关系。

因此，可以说正格矢 $\mathbf{R}_l$ 并没有与之唯一对应的倒格矢 $\mathbf{K}_h$ ，而是有多个倒格矢可以与一个正格矢满足特定的相位关系。

问题5：倒格子是否保持其对应正格子的宏观对称性？

倒格子确实保持了其对应正格子的对称性，但这种对称性是在倒空间（也称为倒易空间）中表现出来的。正格子的对称性通过傅里叶变换转换成倒格子的对称性，因此倒格子的对称操作和正格子的对称操作是相对应的。这意味着，如果正格子具有某种对称性，如旋转对称、反射对称等，其倒格子也将表现出对应的对称性，但这些对称性是在倒格子定义的空间中体现的。

例如，如果一个正格子有简单立方对称性，其倒格子也会有相应的简单立方对称性。然而，对称性的具体表现形式取决于它们是在实空间还是倒空间中考虑的。简而言之，虽然倒格子和正格子的对称性类型相同，但它们的对称元素（如对称轴、对称面）的具体位置和方向可能会有所不同，因为这两种格子分别存在于实空间和倒空间中。