布里渊区(Brillouin Zone)¶
问题:倒格子也是布拉菲格子,那么有无对应的倒空间原胞?
是的,倒格子也是布拉菲格子,因此也有对应的倒空间原胞。在固体物理中,倒格子是用来描述晶体内部电子行为的一个重要工具,特别是在波动性质和能带结构的分析上。每个晶体的布拉菲格子在倒空间中都有一个对应的倒格子,而这个倒格子同样可以定义原胞。
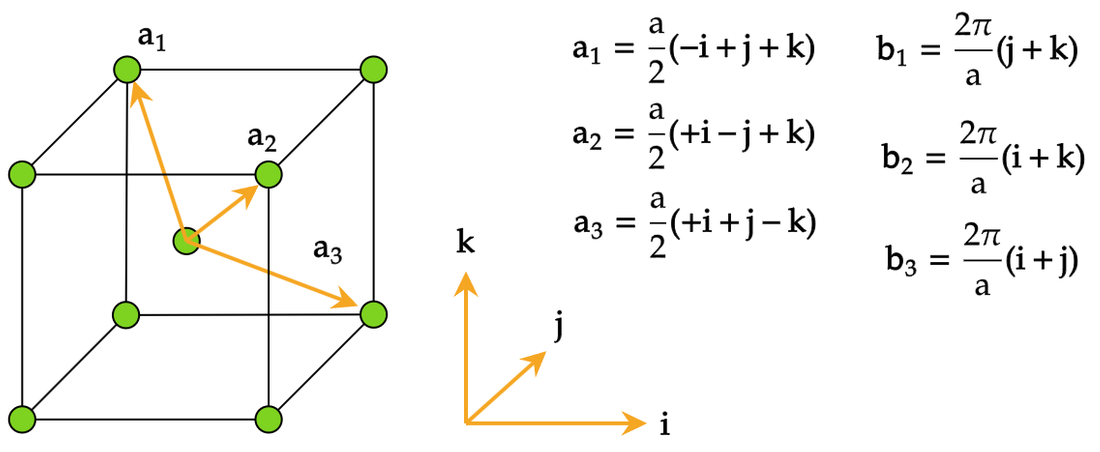
倒格子的定义是基于晶体的直接格子来构造的,目的是为了方便描述和计算晶体中的波动过程。倒格子的基矢与直接格子的基矢满足一定的正交关系。在三维空间中,如果直接格子的基矢是 \(\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\) ,那么倒格子的基矢 \(\mathbf{b}_1, \mathbf{b}_2, \mathbf{b}_3\) 可以通过下列关系定义:
这些倒格子基矢定义了倒空间中的一个单元,称为倒空间原胞,或称为第一布里渊区。这个原胞是倒空间中的最小重复单元,与直接空间中的晶胞相对应。在倒空间中,第一布里渊区常常用来分析晶体的能带结构,因为它包含了晶体的全部不可约表示信息。
倒空间原胞的概念对于理解和计算材料的电子性质至关重要,例如在布洛赫波函数的描述、能带计算以及费米面的研究中都有广泛应用。
在倒空间中,常用的概念是布里渊区而不是倒空间原胞。
倒空间的第一布里渊区是倒空间的 Wigner-Seitz 原胞。
正格子中每个格点代表一个基元,倒格子无这种对应,故在倒空间中,倒空间原胞不常用,常用布里渊区。
下面,我们重新陈述倒空间原胞和布里渊区的概念:
倒空间原胞:倒空间原胞是倒格子的基本单元,与直接空间的晶体原胞相对应。它定义了倒空间中的最小周期性重复单元,可以通过倒格子基矢来界定。任何倒空间中的点都可以通过这些基矢的整数线性组合来表示。倒空间原胞的选择不是唯一的,就像直接空间的晶体原胞一样,有多种方式可以选择倒空间原胞,但其体积是相同的,等于倒格子的基矢构成的平行六面体的体积。

布里渊区:布里渊区是倒空间中的一个特定区域,特别是第一布里渊区,它定义为到最近倒格点的距离小于或等于到任何其他倒格点的距离的所有点的集合。第一布里渊区是电子在晶体中能量带结构分析中最重要的区域,因为它包含了晶体的基本电子性质信息。布里渊区的边界由倒空间中的平面(布拉格平面)构成,这些平面垂直于连接最近邻倒格点的向量的中点(具有极高的对称性,并导致衍射极大)。第一布里渊区可以被视为倒空间原胞的一种特殊选择,它特别重要,因为它与波矢空间中电子态的填充直接相关。
第一布里渊区(一维)¶

第一布里渊区(二维)¶

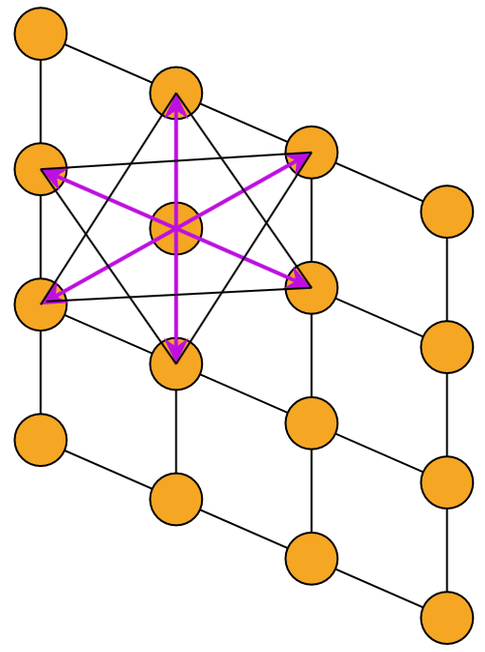
第一布里渊区(体心立方)¶
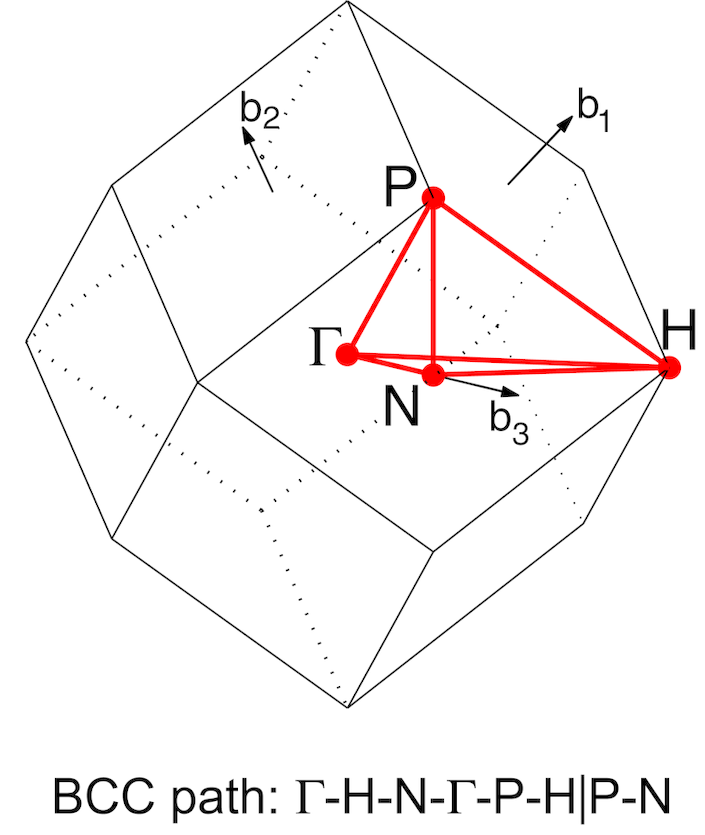
体心立方的倒格子是面心立方。
对顶角的倒格点来说,最近邻的倒格点即 12 个面心格点,所以最短的倒格式显然是指向 12 个面心格点的矢量,它们的中垂面截成正十二面体,正好是倒空间原胞的体积。
第一布里渊区(面心立方)¶
面心立方的倒格子是体心立方。

在倒空间中为第一布里渊区为:
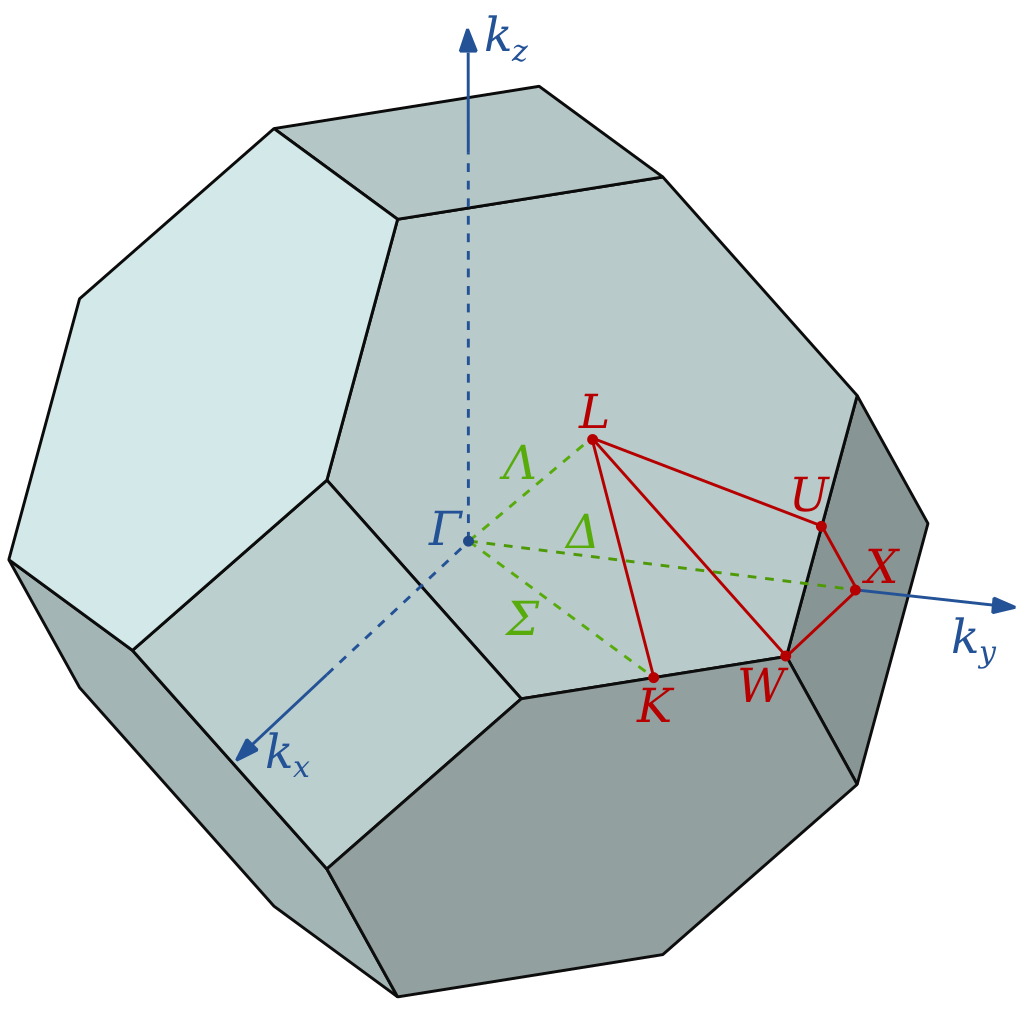
对于位于中心的倒格点,与之最接近的倒格点是位于八个角落的点。因此,连接中心点和这八个角点的最短倒格向量自然定义了向这些角落指向的方向,其构成的中垂平面将空间划分成一个八面体形状。然而,这个八面体的体积相对较大,需要进一步进行切割以得到第一布里渊区。显然,次近邻的倒格点位于相邻晶胞的体心位置。通过在\(k_x\)、\(k_y\)和\(k_z\)轴方向上切割六个中垂平面,我们可以获得一个更精细的结构,这样切割后得到的便是面心立方晶体在倒空间中的第一布里渊区。
我们发现:第一布里渊区不一定是最近邻倒格点的中垂面所围。