谐振子与 Hermite 多项式
本文主要参考书籍:
曾谨言著. 2013. 量子力学. 卷Ⅰ | 5版[M]. 北京:科学出版社
孙婷雅 编. 2004. 量子力学教程习题剖析[M]. 北京:科学出版社
Bruce Cameron Reed. 2022. Quantum Mechanics: An Enhanced Primer [M]. Springer Cham.
背景
在数学中,Hermite 多项式(Hermite polynomials)是一种经典的正交多项式族,得名于法国数学家夏尔·埃尔米特(Charles Hermite)。
在概率论中,埃奇沃斯级数的表达式中就要用到 Hermite 多项式。
在组合数学中,Hermite 多项式是阿佩尔方程的解。
子啊物理学中,Hermite 多项式给出了量子谐振子的本征态。
 Charles Hermite
Charles Hermite
图片链接
在概率论中常用的形式:
\[\displaystyle H_{n}^{\mathrm{prob} }(x)=(-1)^{n} e^{\frac{x^{2}}{2}} \frac{d^{n}}{d x^{n}} e^{-\frac{x^{2}}{2}}\]
在物理学中常用的形式:
\[\displaystyle H_{n}^{\mathrm{phys} }(x)=(-1)^{n} e^{x^{2}} \frac{d^{n}}{d x^{n}} e^{-x^{2}}\]
两种形式之间的转化关系:
\[\displaystyle H_{n}^{\text {phys }}(x)=2^{\frac{n}{2}} H_{n}^{\text {prob }}(\sqrt{2} x)\]
前六个概率学和物理学中的 Hermite 多项式:
\[\begin{array}{|l|l|l|}\hline \bf{序号} & \bf{概率学} & \bf{物理学} \\\hline H_{0}(x) & 1 & 1 \\\hline H_{1}(x) & x & 2x \\\hline H_{2}(x) & x^{2}-1 & 4x^{2}-2 \\\hline H_{3}(x) & x^{3}-3x & 8x^{3}-12x \\\hline H_{4}(x) & x^{4}-6x^{2}+3 & 16x^{4}-48x^{2}+12 \\\hline H_{5}(x) & x^{5}-10x^{3}+15x & 32x^{5}-160x^{3}+120x \\\hline\end{array}\]
前 11 个概率学中的 Hermite 多项式:
\[\begin{array}{l}H e_{0}(x)=1 \\H e_{1}(x)=x \\H e_{2}(x)=x^{2}-1 \\H e_{3}(x)=x^{3}-3 x \\H e_{4}(x)=x^{4}-6 x^{2}+3 \\H e_{5}(x)=x^{5}-10 x^{3}+15 x \\H e_{6}(x)=x^{6}-15 x^{4}+45 x^{2}-15 \\H e_{7}(x)=x^{7}-21 x^{5}+105 x^{3}-105 x \\H e_{8}(x)=x^{8}-28 x^{6}+210 x^{4}-420 x^{2}+105 \\H e_{9}(x)=x^{9}-36 x^{7}+378 x^{5}-1260 x^{3}+945 x \\H e_{10}(x)=x^{10}-45 x^{8}+630 x^{6}-3150 x^{4}+4725 x^{2}-945\end{array}\]
 前 6 个概率学中的 Hermite 多项式
前 6 个概率学中的 Hermite 多项式
图片链接
前 11 个物理学中的 Hermite 多项式:
\[\begin{array}{l}H_{0}(x)=1 \\H_{1}(x)=2 x \\H_{2}(x)=4 x^{2}-2 \\H_{3}(x)=8 x^{3}-12 x \\H_{4}(x)=16 x^{4}-48 x^{2}+12 \\H_{5}(x)=32 x^{5}-160 x^{3}+120 x \\H_{6}(x)=64 x^{6}-480 x^{4}+720 x^{2}-120 \\H_{7}(x)=128 x^{7}-1344 x^{5}+3360 x^{3}-1680 x \\H_{8}(x)=256 x^{8}-3584 x^{6}+13440 x^{4}-13440 x^{2}+1680 \\H_{9}(x)=512 x^{9}-9216 x^{7}+48384 x^{5}-80640 x^{3}+30240 x \\H_{10}(x)=1024 x^{10}-23040 x^{8}+161280 x^{6}-403200 x^{4}+302400 x^{2}-30240\end{array}\]
 前 6 个物理学中的 Hermite 多项式
前 6 个物理学中的 Hermite 多项式
图片链接
理论推导
建立微分方程
一维谐振子受到的线性恢复力:
\[F=-k x \quad(-\infty \leq x \leq \infty)\]
这种系统的经典模型是质量 \(m\) 附着在力常数为 \(k\) 的弹簧上。如果弹簧从其平衡位置拉伸(或压缩)一个位移 \(x\) ,它将以与 \(x\) 成比例的力向后拉(或推动),结果是正弦简谐运动,以周期 \(\displaystyle T=2 \pi \sqrt{\frac{m}{k}}\) 秒重复。在原子水平上,双原子分子的行为非常接近于两个原子核通过弹簧连接。
对应于线性恢复力的电势通过对力方程进行积分而获得(谐振子电势):
\[\displaystyle V(x)=-\int F d x=\int k x d x=\frac{kx^{2}}{2}+c\]
其中 \(c\) 是积分常数。
通常,常数 \(c\) 不再被进一步考虑,因为 \(c\) 的非零值的效果将是将允许的能级提高或降低该量,只有势能的差异在物理上是有意义的。
对应的薛定谔方程为:
\[\displaystyle -\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi(x)}{d x^{2}}+\frac{1}{2} k x^{2} \psi(x)=E \psi(x)\]
我们假设谐振子的质量为 \(\mu\),并令 \(\displaystyle \omega_{0}=\sqrt{\frac{k}{\mu}}\),则哈密顿量可以表示为:
\[\displaystyle H=\frac{p_{x}^{2}}{2 \mu}+\frac{1}{2} \mu \omega_{0}^{2} x^{2}\]
则薛定谔方程还可以写为:
\[\displaystyle \left(-\frac{\hbar^{2}}{2 \mu} \frac{\mathrm{d}^{2}}{\mathrm{~d} x^{2}}+\frac{1}{2} \mu \omega_{0}^{2} x^{2}\right) \psi(x)=E \psi(x)\]
注:严格的谐振子势是一个无限深势阱,粒子只存在束缚态,当 \(|x| \rightarrow \infty\) 的时候,波函数 \(\psi(x)\to 0\)。
引入无量纲参数:
\[
\begin{array}{ll}z=\alpha x\\\displaystyle \alpha=\sqrt{\frac{\mu \omega_{0}}{\hbar}}\\\displaystyle \lambda=E / \frac{1}{2} \hbar \omega_{0}\end{array}
\]
则一维谐振子的薛定谔方程可以写为:
\[\displaystyle \frac{\mathrm{d}^{2}}{\mathrm{~d} z^{2}} \psi+\left(\lambda-z^{2}\right) \psi=0\]
近似解
因为谐振子是束缚态,在 \(|x| \rightarrow \infty\),即 \(|z|\to\infty\) 的时候,\(\psi(x)\to 0\)。
当 \(|\xi|\to\infty\) 时,方程 \(\displaystyle \frac{\mathrm{d}^{2}}{\mathrm{~d} z^{2}} \psi+\left(\lambda-z^{2}\right) \psi=0\) 可以近似表示为:
\[\displaystyle \frac{\mathrm{d}^{2}}{\mathrm{~d} z^{2}} \psi-z^{2} \psi=0\]
因为解是束缚态,所以我们猜测的解的形式为:
\[\psi(z) \sim A \exp \left(\beta z^{n}\right), \quad(z \rightarrow \pm \infty)\]
其中 \(A\)、\(B\) 和 \(n\) 有待确定。
将猜测的解带入 \(\displaystyle \frac{d^{2} \psi(z)}{d z^{2}}\),我们可以得到:
\[\displaystyle \frac{d^{2} \psi(z)}{d z^{2}}=\left[n^{2} \beta^{2} z^{2 n-2}+n(n-1) \beta z^{n-2}\right] \psi(z)\]
带回公式 \(\displaystyle \frac{\mathrm{d}^{2}}{\mathrm{~d} z^{2}} \psi-z^{2} \psi=0\),我们可以发现:
\[\displaystyle n^{2} \beta^{2} z^{2 n-2}+n(n-1) \beta z^{n-2} \sim z^{2}\]
除非上述公式 \(z\) 的幂次是一样的,否则上式没有意义。
我们不考虑负幂的情况(否则原点就是无穷大),则 \(n\) 一定是正的。
对于 \(z\rightarrow \pm \infty\) 情况,公式左侧 \(n^{2} \beta^{2} z^{2 n-2}\) 占据主导,我们可以给出:
\[n^{2} \beta^{2} z^{2 n-2} \sim z^{2}\]
当 \(2 n-2=2\) 或 \(n=2\) 的时候,\(z\) 的幂次才正常。
并且在 \(n^{2} \beta^{2}=1\) 或 \(\displaystyle \beta= \pm \frac{1}{2}\) 时,系数才可以校准。
当 \(\displaystyle \beta= \frac{1}{2}\) 时,渐进解的形式为:\(\displaystyle \psi(z) \propto \exp \left(\frac{z^{2}}{2}\right)\)
这样的解不可能归一化,所以最后的解只有在 \(\displaystyle \beta=-\frac{1}{2}\) 时才可以存在:
\[\displaystyle \psi(z) \sim A \exp \left(-\frac{z^{2}}{2}\right), \quad(z \rightarrow \pm \infty)\]
此时,我们还有系数 \(A\) 没有解出来。但是我们现在我们只有近似解,在精确求解的时候,前面的系数可能改变,所以系数 \(A\) 我们可以稍后处理。
精确解
我们希望精确解的求解过程可以建立在上面近似解的基础上。
我们可以假设 \(\psi\) 可以表示为两个函数的乘积,其中一项是上面的近似解,另一项是未知函数 \(u(z)\):
\[\displaystyle \psi(z)=\exp \left(-\frac{1}{2} z^{2}\right) u(z)\]
我们如何知道这是否是一个有效的假设?
答案是我们没有,至少现在还没有。就像在任何试错的情况下一样,只有在事后看看它是否能起作用,才能知道是否有效。
\(u(z)\) 的具体形式是什么?
从初等微积分中我们可以知道,\(z\) 的任何函数形式都可以表示为泰勒级数或麦克劳林级数展开式。
我们可以将 \(u(z)\) 进行泰克展开:
在 \(z=0\) 点领域(\(|z|<\infty\) 范围)中,对 \(u(z)\) 作泰勒展开:
\[\displaystyle u(z)=\sum_{k=0}^{\infty} C_{k} z^{k}\]
注:这里我们默认 \(u(z)\) 是没有负幂的,因为负幂项会导致在 \(z=0\) 点存在无穷大。虽然无穷大不会影响 \(u(z)\) 的合理性(只要 \(u(z)\) 是归一化的),但在这里我们忽略存在负幂的情况。
将我们假设的解 \(\displaystyle \psi(z)=\exp \left(-\frac{1}{2} z^{2}\right) u(z)\) 带入 $\displaystyle \frac{\mathrm{d}^{2}\psi}{\mathrm{~d} z^{2}} $,我们可以得到:
\[\displaystyle \frac{d^{2} \psi}{d z^{2}}=\left(\frac{d^{2} H}{d z^{2}}-2 z \frac{d H}{d z}+\left(z^{2}-1\right) H\right) e^{-\frac{z^{2}}{2}}\]
再将 $\displaystyle \frac{\mathrm{d}^{2}\psi}{\mathrm{~d} z^{2}} $ 的具体形式带入薛定谔方程 \(\displaystyle \frac{\mathrm{d}^{2}}{\mathrm{~d} z^{2}} \psi+\left(\lambda-z^{2}\right) \psi=0\),并消除常见的指数因子,我们可以得到 \(u(z)\) 的微分方程:
\[u^{\prime \prime}-2 z u^{\prime}+(\lambda-1) u=0\]
这就是 Hermite 方程。
\(\displaystyle u(z)=\sum_{k=0}^{\infty} C_{k} z^{k}\) 的一阶导数和二阶导数的具体形式为:
\[
\begin{array}{ll}\displaystyle \frac{d u}{d z}=\sum_{k=0}^{\infty} k C_{k} z^{k-1}\\\displaystyle \frac{d^{2} u}{d z^{2}}=\sum_{n=0}^{\infty} k(k-1) C_{k} z^{k-2}\end{array}
\]
将 \(\displaystyle u(z)=\sum_{k=0}^{\infty} C_{k} z^{k}\)、\(\displaystyle \frac{d u}{d z}=\sum_{k=0}^{\infty} k C_{k} z^{k-1}\) 和 \(\displaystyle \frac{d^{2} u}{d z^{2}}=\sum_{n=0}^{\infty} k(k-1) C_{k} z^{k-2}\) 带入薛定谔方程 \(u^{\prime \prime}-2 z u^{\prime}+(\lambda-1) u=0\),我们可以得到:
\[\displaystyle \sum_{k=0}^{\infty} k(k-1) C_{k} \xi^{k-2}+\sum_{k=0}^{\infty}[\lambda-1-2 k] C_{k} \xi^{k}=0\]
我们发现在 \(k=0,1\) 的项为零:
\[\displaystyle \sum_{k=0}^{\infty} k(k-1) C_{k} z^{k-2}=0+0+\sum_{k=2}^{\infty} k(k-1) C_{k} z^{k-2}\]
为了从 0 开始计数,我们定了一个新的索引 \(j=k-2\),则上式可以写成:
\[\displaystyle \sum_{k=0}^{\infty} k(k-1) C_{k} z^{k-2}=\sum_{k=2}^{\infty} k(k-1) C_{k} z^{k-2}=\sum_{j=0}^{\infty}(j+2)(j+1) C_{j+2} z^{j}\]
由于 \(k\) 和 \(j\) 都是伪索引,我们可以将 \(j\) 重新标记为 \(k\)(就是换个符号表示而已)。
\[\displaystyle \sum_{k=0}^{\infty} k(k-1) C_{k} z^{k-2}=\sum_{k=0}^{\infty}(k+2)(k+1) C_{k+2} z^{k}\]
将上式带入 \(\displaystyle \sum_{k=0}^{\infty} k(k-1) C_{k} \xi^{k-2}+\sum_{k=0}^{\infty}[\lambda-1-2 k] C_{k} \xi^{k}=0\),我们可以得到:
\[\displaystyle \sum_{k=0}^{\infty}\left[(k+1)(k+2) C_{k+2}+(\lambda-1-2 k) C_{k}\right] z^{k}=0\]
这种指数过程的变换是常用于微分方程级数解的一种有用技巧。
从上式,我们可以解出 \(C_k\) 之间的递推关系:
\[\displaystyle C_{k+2}=\frac{2 k-(\lambda-1)}{(k+2)(k+1)} C_{k}, \quad k=0,1,2, \cdots\]
因此,所有偶次幂项的系数都可以用 \(C_0\) 表示,所有奇次幂项系数都可以用 \(C_1\) 表示。
\(C_0\) 和 \(C_1\) 是两个任意常数,从而求得方程 \(u^{\prime \prime}-2 z u^{\prime}+(\lambda-1) u=0\) 的两个线性无关的解:
\[\begin{array}{l}u_{1}(z)=C_{0}+C_{2} z^{2}+C_{4} z^{4}+\cdots \\u_{2}(z)=C_{1} z+C_{3} z^{3}+C_{5} z^{5}+\cdots\end{array}\]
当 \(z\) 为有限值的时候,上述两个式子都收敛。
但在 \(|z| \rightarrow \infty\) 时有问题。
通过公式 \(\displaystyle C_{k+2}=\frac{2 k-(\lambda-1)}{(k+2)(k+1)} C_{k}\),我们可以发现:
当 \(k \rightarrow \infty\) 的时候,\(\displaystyle \frac{C_{k+2}}{C_{k}}\approx \frac{2}{k}\);
当 \(k=2m\)(偶数)的时候,\(\displaystyle \frac{C_{2 m+2}}{C_{2 m}} \approx \frac{1}{m}\);
\(\exp \left(z^{2}\right)\) 的泰勒展开:\(\displaystyle \exp \left(z^{2}\right)=\sum_{m=0}^{\infty} \frac{z^{2 m}}{m !}\)
\(k=2m\) 时,我们发现 \(u_1(z)\) 相邻项系数的比值与 \(\exp \left(z^{2}\right)\) 相邻项系数的比值相同。
因此,当 \(|z| \rightarrow \infty\) 时,\(u_1(z)\) 的发散行为与 \(\exp \left(z^{2}\right)\) 相同。
同理,当 \(|z| \rightarrow \infty\) 时,\(u_2(z)\) 的发散行为与 \(z\exp \left(z^{2}\right)\) 相同。
这样的解带入谐振子波函数 \(\displaystyle \psi \propto \exp \left(-\frac{1}{2} \xi^{2}\right) u(\xi)\) 都不满足波函数在无穷远点的边界条件。
因此,为了得到物理上允许的解,我们必须要求 \(u_1(z)\) 和 \(u_2(z)\) 两个级数解中至少有一个为中断多项式。
根据公式 \(\displaystyle C_{k+2}=\frac{2 k-(\lambda-1)}{(k+2)(k+1)} C_{k}\),我们可以发现,当 \(\lambda-1=2 n\)(\(n=0,1,2, \cdots\))时,级数将中断为多项式。
此时,\(C_{n+2}\)、\(C_{n+4}\)、\(C_{n+6}\)、......都将为零。
当 \(n\) 为偶数的时候,\(u_1(z)\) 中断为多项式,\(u_2(z)\) 仍为无穷级数。
当 \(n\) 为奇数的时候,\(u_2(z)\) 中断为多项式,\(u_1(z)\) 仍为无穷级数。
但无论如何(不论 \(n\) 为偶数或奇数),只要 \(\lambda-1=2 n\) 成立,我们就找到了一个多项式解。
将 \(\lambda-1=2 n\) 带入谐振子波函数 \(\displaystyle \psi \propto \exp \left(-\frac{1}{2} z^{2}\right) u(z)\) ,我们也就找到了在物理上允许的一个谐振子波函数。
当 \(\lambda-1=2 n\) 成立时,Hermite 方程 \(u^{\prime \prime}-2 z u^{\prime}+(\lambda-1) u=0\) 有一个多项式解(另一个解为无穷级数)。
习惯上规定其最高次项系数 \(C_{n}=2^{n}\),这样的多项式称为 Hermite 多项式。
把 \(\lambda-1=2 n\) 带入 \(\displaystyle C_{k+2}=\frac{2 k-(\lambda-1)}{(k+2)(k+1)} C_{k}\),我们可以得到:
\[\displaystyle C_{k}=-\frac{(k+2)(k+1)}{2(n-k)} C_{k+2}\]
为了方便,我们进行替换 \(k \rightarrow n-k\),上式可以修改为:
\[\displaystyle C_{n-k}=-\frac{(n-k+2)(n-k+1)}{2 k} C_{n-k+2}\]
取 \(C_{n}=2^{n}\),并依次令 \(k=2,4,6, \cdots,\)得出:
\[\begin{array}{l}\displaystyle C_{n-2}=-n(n-1) \cdot 2^{n-2} \\\displaystyle C_{n-4}=+\frac{n(n-1)(n-2)(n-3)}{2 !} 2^{n-4} \\\displaystyle C_{n-6}=-\frac{n(n-1)(n-2)(n-3)(n-4)(n-5)}{3 !} 2^{n-6} \\\cdots \end{array}\]
因此
\[\begin{aligned}\mathrm{H}_{n}(z)= & (2 z)^{n}-n(n-1)(2 z)^{n-2}+\frac{n(n-1)(n-2)(n-3)}{2 !}(2 z)^{n-4}-\cdots+\cdots+(-1)^{\left[\frac{n}{2}\right]} \cdot \frac{n !}{\left[\frac{n}{2}\right] !}(2 z)^{n-2\left[\frac{n}{2}\right]}\end{aligned}\]
其中 \(\displaystyle \left[\frac{n}{2}\right]\) 表示不大于 \(\displaystyle \frac{n}{2}\) 的最大整数,具体形式为:
\[\displaystyle \left[\frac{n}{2}\right]=\left\{\begin{array}{ll}\displaystyle \frac{n}{2} &\displaystyle (n \text { 为偶数 }) \\\displaystyle \frac{n-1}{2} &\displaystyle (n \text { 为奇数 })\end{array}\right.\]
此即 Hermite 多项式。
可以证明,Hermite 多项式的生成函数(generating function)为:
\[\displaystyle \exp \left(-s^{2}+2 z s\right)=\sum_{n=0}^{\infty} \frac{\mathrm{H}_{n}(z)}{n !} s^{n}\]
因此
\[\begin{aligned}\mathrm{H}_{n}(z) & =\left.\frac{\mathrm{d}^{n}}{\mathrm{~d} s^{n}} \exp \left(-s^{2}+2 z s\right)\right|_{s=0}\\&=\left.\exp \left(z^{2}\right) \cdot \frac{\mathrm{d}^{n}}{\mathrm{~d} s^{n}} \exp \left[-(s-z)^{2}\right]\right|_{s=0} \\& =\left.(-1)^{n} \exp \left(z^{2}\right) \cdot \frac{\mathrm{d}^{n}}{\mathrm{~d} z^{n}} \exp \left[-(s-z)^{2}\right]\right|_{s=0}\end{aligned}\]
所以
\[\displaystyle \mathrm{H}_{n}(z)=(-1)^{n} \exp \left(z^{2}\right) \frac{\mathrm{d}^{n}}{\mathrm{~d} z^{n}} \exp \left(-z^{2}\right)\]
不难直接验证,上式给出的 \(\mathrm{H}_{n}(z)\) 确实是微分方程 \(u^{\prime \prime}-2 z u^{\prime}+(\lambda-1) u=0\) 的解。
其次,公式 \(\displaystyle \mathrm{H}_{n}(z)=(-1)^{n} \exp \left(z^{2}\right) \frac{\mathrm{d}^{n}}{\mathrm{~d} z^{n}} \exp \left(-z^{2}\right)\) 是一个 \(n\) 次多项式。
因为对 \(\exp \left(-z^{2}\right)\) 求导一次,就多出一个含 \(z\) 的项。
例如:\(\displaystyle \frac{\mathrm{d}}{\mathrm{d} z} \exp \left(-z^{2}\right)=-2 z \exp \left(-z^{2}\right)\)
对 \(\exp \left(-z^{2}\right)\) 进行 \(n\) 次求导后,多项式 \(\mathrm{H}_{n}(z)\) 的最高次项将是:
\[\displaystyle (-1)^{n} \cdot \exp \left(z^{2}\right) \cdot(-2 z)^{n} \cdot \exp \left(-z^{2}\right)=2^{n} \cdot z^{n}\]
这与下述公式最高次项的结果相同:
\[\begin{aligned}\mathrm{H}_{n}(z)= & (2 z)^{n}-n(n-1)(2 z)^{n-2}+\frac{n(n-1)(n-2)(n-3)}{2 !}(2 z)^{n-4}-\cdots+\cdots+(-1)^{\left[\frac{n}{2}\right]} \cdot \frac{n !}{\left[\frac{n}{2}\right] !}(2 z)^{n-2\left[\frac{n}{2}\right]}\end{aligned}\]
对于一定的 \(n\),微分方程 \(u^{\prime \prime}-2 z u^{\prime}+(\lambda-1) u=0\) 的多项式解只有一个。
因此
\[\begin{aligned}\mathrm{H}_{n}(z)= & (2 z)^{n}-n(n-1)(2 z)^{n-2}+\frac{n(n-1)(n-2)(n-3)}{2 !}(2 z)^{n-4}-\cdots+\cdots+(-1)^{\left[\frac{n}{2}\right]} \cdot \frac{n !}{\left[\frac{n}{2}\right] !}(2 z)^{n-2\left[\frac{n}{2}\right]}\end{aligned}\]
与
\[\displaystyle \mathrm{H}_{n}(z)=(-1)^{n} \exp \left(z^{2}\right) \frac{\mathrm{d}^{n}}{\mathrm{~d} z^{n}} \exp \left(-z^{2}\right)\]
全同。
正交性
利用公式 \(\displaystyle \exp \left(-s^{2}+2 z s\right)=\sum_{n=0}^{\infty} \frac{\mathrm{H}_{n}(z)}{n !} s^{n}\) 或 \(\displaystyle \mathrm{H}_{n}(z)=(-1)^{n} \exp \left(z^{2}\right) \frac{\mathrm{d}^{n}}{\mathrm{~d} z^{n}} \exp \left(-z^{2}\right)\),都不难证明 Hermite 多项式的正交性公式为:
\[\displaystyle \int_{-\infty}^{+\infty} \mathrm{H}_{m}(z) \mathrm{H}_{n}(z) \exp \left(-z^{2}\right) \mathrm{d} z=\sqrt{\pi} 2^{n} \cdot n ! \delta_{m n}\]
\(\exp \left(-z^{2}\right)\) 称为权重因子。
下面用生成函数 \(\displaystyle \exp \left(-s^{2}+2 z s\right)=\sum_{n=0}^{\infty} \frac{\mathrm{H}_{n}(z)}{n !} s^{n}\) 来证明。
利用
\[\begin{array}{l}\displaystyle \exp \left(-t^{2}+2 z t\right)=\sum_{m=0}^{\infty}\frac{\mathrm{H}_{m}(z) t^{m}}{m !} \\\displaystyle \exp \left(-s^{2}+2 z s\right)=\sum_{n=0}^{\infty}\frac{\mathrm{H}_{n}(z) s^{n}}{n !}\end{array}\]
相乘得到
\[\begin{aligned}\exp \left[-\left(t^{2}+s^{2}\right)+2 z(t+s)\right] & =\exp \left(2 t s+z^{2}\right) \cdot \exp \left[-(t+s-z)^{2}\right] \\& =\sum^{\infty}_{m,n=0} \frac{\mathrm{H}_{m}(z) \mathrm{H}_{n}(z) t^{m} s^{n}}{m ! n !}\end{aligned}\]
两边乘以 \(\exp \left(-z^{2}\right)\) 并积分
\[\displaystyle \exp (2 t s) \int_{-\infty}^{+\infty} \exp \left[-(z-t-s)^{2}\right] \mathrm{d} z=\sum_{m, n=0}^{\infty} \frac{t^{m} s^{n}}{m ! n !} \cdot \int_{-\infty}^{+\infty} \mathrm{H}_{m}(z) \mathrm{H}_{n}(z) \exp \left(-z^{2}\right) \mathrm{d} z\]
上式的左边部分
\[\begin{aligned}\exp (2 t s) \int_{-\infty}^{+\infty} \exp \left[-(z-t-s)^{2}\right] \mathrm{d} z& =\exp (2 t s) \int_{-\infty}^{+\infty} \exp \left(-\xi^{2}\right) \mathrm{d} \xi \\& =\exp (2 t s) \sqrt{\pi}\\&=\sqrt{\pi} \sum_{n=0}^{\infty} \frac{(2 t s)^{n}}{n !}\end{aligned}\]
所以我们可以得到:
\[\displaystyle \sqrt{\pi} \sum_{n=0}^{\infty} \frac{(2 t s)^{n}}{n !}=\sum_{m, n=0}^{\infty} \frac{t^{m} s^{n}}{m ! n !} \cdot \int_{-\infty}^{+\infty} \mathrm{H}_{m}(z) \mathrm{H}_{n}(z) \exp \left(-z^{2}\right) \mathrm{d} z\]
\[\displaystyle \Rightarrow \int_{-\infty}^{+\infty} \mathrm{H}_{m}(z) \mathrm{H}_{n}(z) \exp \left(-z^{2}\right) \mathrm{d} z=\sqrt{\pi} 2^{n} \cdot n ! \delta_{m n}\]
递推关系
生成函数式 \(\displaystyle \exp \left(-s^{2}+2 z s\right)=\sum_{n=0}^{\infty} \frac{\mathrm{H}_{n}(z)}{n !} s^{n}\) 两边对 \(s\) 求导,我们可以得到:
\[\begin{array}{l}\displaystyle \text { 左边 }=(-2 s+2 z) \exp \left(-s^{2}+2 z s\right)=(-2 s+2 z) \sum_{n=0}^{\infty} \frac{\mathrm{H}_{n}(z)}{n !} s^{n} \\\displaystyle \text { 右边 }=\sum_{n=1}^{\infty} \frac{\mathrm{H}_{n}(z)}{n !} n s^{n-1}=\sum_{n=0}^{\infty} \frac{\mathrm{H}_{n+1}(z)}{n !} s^{n}\end{array}\]
比较两边 \(s\) 同幂项的系数,我们就可以得到 Hermite 多项式的递推关系:
\[\mathrm{H}_{n+1}(z)-2 z \mathrm{H}_{n}(z)+2 n \mathrm{H}_{n-1}(z)=0\]
同理,对生成函数式 \(\displaystyle \exp \left(-s^{2}+2 z s\right)=\sum_{n=0}^{\infty} \frac{\mathrm{H}_{n}(z)}{n !} s^{n}\) 两边对 \(z\) 求导,我们可以得到:
\[\mathrm{H}_{n}^{\prime}(z)=2 n \mathrm{H}_{n-1}(z)\]
谐振子
将 \(\lambda-1=2 n\) 带入 \(\displaystyle \lambda=E / \frac{1}{2} \hbar \omega_{0}\),我们可以得到:
\[\displaystyle E=E_{n}=\left(n+\frac{1}{2}\right) \hbar \omega_{0}, \quad n=0,1,2, \cdots\]
这就是谐振子能量可能的取值,即能量本征值。
由于谐振子是束缚态,所以能量是量子化的。
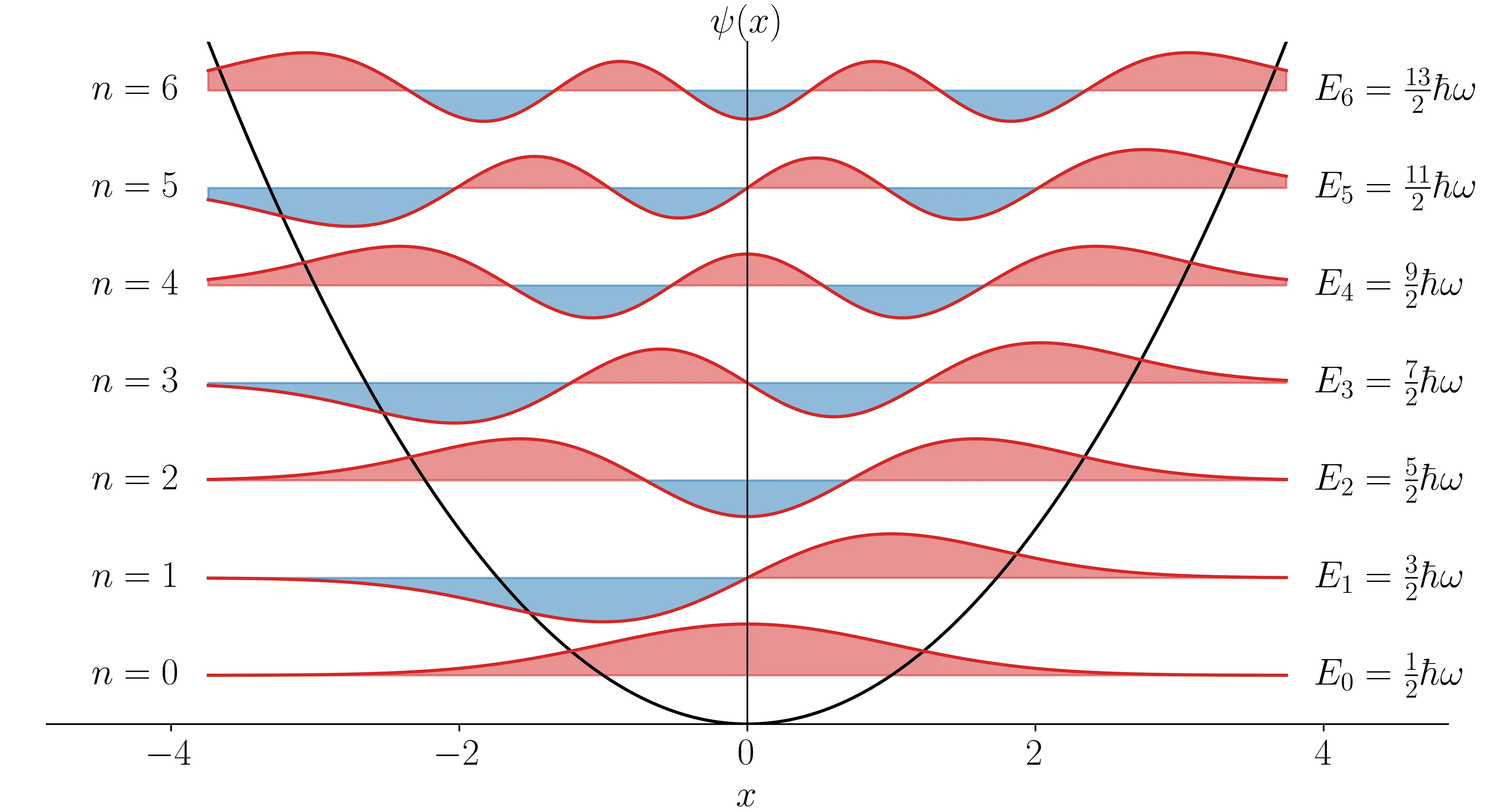 一维谐振子
一维谐振子
图片链接
谐振子能量是均匀分布的,相邻能级之间差 \(\hbar \omega_{0}\)。
谐振子的基态能量(零点能)为:\(\displaystyle E_{0}=\frac{1}{2} \hbar \omega_{0}\)
\[\begin{aligned}\mathrm{H}_{n}(z)= & (2 z)^{n}-n(n-1)(2 z)^{n-2}+\frac{n(n-1)(n-2)(n-3)}{2 !}(2 z)^{n-4}-\cdots+\cdots+(-1)^{\left[\frac{n}{2}\right]} \cdot \frac{n !}{\left[\frac{n}{2}\right] !}(2 z)^{n-2\left[\frac{n}{2}\right]}\end{aligned}\]
上式是谐振子的一个解(另外一个解是无穷级数)。
前 11 个 Hermite 多项式:
\[\begin{aligned}H_{0}(z) & =1 \\H_{1}(z) & =2 z \\H_{2}(z) & =4 z^{2}-2 \\H_{3}(z) & =8 z^{3}-12 z \\H_{4}(z) & =16 z^{4}-48 z^{2}+12 \\H_{5}(z) & =32 z^{5}-160 z^{3}+120 z \\H_{6}(z) & =64 z^{6}-480 z^{4}+720 z^{2}-120 \\H_{7}(z) & =128 z^{7}-1344 z^{5}+3360 z^{3}-1680 z \\H_{8}(z) & =256 z^{8}-3584 z^{6}+13440 z^{4}-13440 z^{2}+1680 \\H_{9}(z) & =512 z^{9}-9216 z^{7}+48384 z^{5}-80640 z^{3}+30240 z \\H_{10}(z) & =1024 z^{10}-23040 z^{8}+161280 z^{6}-403200 z^{4}+302400 z^{2}-30240\end{aligned}\]
利用正交公式:
\[\displaystyle \int_{-\infty}^{+\infty} \mathrm{H}_{m}(z) \mathrm{H}_{n}(z) \exp \left(-z^{2}\right) \mathrm{d} z=\sqrt{\pi} 2^{n} \cdot n ! \delta_{m n}\]
我们可以得到归一化的谐振子波函数(实函数):
\[\begin{array}{l}\displaystyle \psi_{n}(x)=N_{n} \exp \left(-\frac{1}{2} \alpha^{2} x^{2}\right) \mathrm{H}_{n}(a x) \\\displaystyle N_{n}=\left(\frac{\alpha}{\sqrt{\pi} 2^{n} n !}\right)^{\frac{1}{2}} \quad(\text { 归一化常数 }) \\\displaystyle \int_{-\infty}^{+\infty} \psi_{m}(x) \psi_{n}(x) \mathrm{d} x=\delta_{m n}\end{array}\]
谐振子前四条能级的的能量本征函数:
\[\begin{array}{ll}\displaystyle \psi_{0}(x)=\frac{\sqrt{\alpha}}{\pi^{1 / 4}} \exp \left(-\frac{1}{2} \alpha^{2} x^{2}\right)\\\displaystyle \psi_{1}(x)=\frac{\sqrt{2 \alpha}}{\pi^{1 / 4}} \alpha x \exp \left(-\frac{1}{2} \alpha^{2} x^{2}\right) \\\displaystyle \psi_{2}(x)=\frac{1}{\pi^{1 / 4}} \sqrt{\frac{\alpha}{2}}\left(2 \alpha^{2} x^{2}-1\right) \exp \left(-\frac{1}{2} \alpha^{2} x^{2}\right) \\\displaystyle \psi_{3}(x)=\frac{\sqrt{3 \alpha}}{\pi^{1 / 4}} \alpha x\left(\frac{2}{3} \alpha^{2} x^{2}-1\right) \exp \left(-\frac{1}{2} \alpha^{2} x^{2}\right)\end{array}\]
我们还可以发现能量本征函数的奇偶性与 \(n\) 有关:
\[\psi_{n}(-x)=(-1)^{n} \psi_{n}(x)\]
性质分析
基态
 基态的能量和概率分布
基态的能量和概率分布
基态能量:\(\displaystyle E_{0}=\frac{1}{2} \hbar \omega_{0}\)
基态概率分布:\(\displaystyle \left|\psi_{0}(x)\right|^{2}=\frac{\alpha}{\sqrt{\pi}} \exp \left(-\alpha^{2} x^{2}\right)\)
在 \(x=0\) 处出现谐振子的概率最大。
从经典力学出发,粒子将限制在 \(|\alpha x| \leqslant 1\) 范围中运动,因为在 \(|\alpha x| = 1\) 处势能等于能量(粒子速度为 0):
\[\displaystyle V(x)=\frac{1}{2} k x^{2}=\frac{1}{2} k / \alpha^{2}=\frac{1}{2} \hbar \omega_{0}\]
从量子力学出发,在经典禁区 \(|\alpha x|>1\) 中,\(\psi_{0}(x)\) 并不为零,粒子有一定概率在禁区出现。
对于基态,出现的概率为:
\[\frac{\displaystyle \int_{1}^{\infty} \exp \left(-\xi^{2}\right) \mathrm{d} \xi}{\displaystyle \int_{0}^{\infty} \exp \left(-\xi^{2}\right) \mathrm{d} \xi} \approx 16 \%\]
谐振子的不确定系关系
已知
\[\begin{array}{c}\mathrm{H}_{n+1}(x)-2 x \mathrm{H}_{n}(x)+2 n \mathrm{H}_{n-1}(x)=0 \\\displaystyle\psi_{n}(x)=\left(\frac{\alpha}{\sqrt{\pi} 2^{n} n !}\right)^{\frac{1}{2}} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}} \mathrm{H}_{n}(\alpha x) \\\displaystyle\psi_{n+1}(x)=\left(\frac{\alpha}{\sqrt{\pi} 2^{n+1}(n+1) !}\right)^{\frac{1}{2}} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}} \mathrm{H}_{n+1}(\alpha x) \\\displaystyle\psi_{n-1}(x)=\left(\frac{\alpha}{\sqrt{\pi} 2^{n-1}(n-1) !}\right)^{\frac{1}{2}} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}} \mathrm{H}_{n-1}(\alpha x)\end{array}\]
所以
\[\begin{aligned}x \psi_{n}(x)= & \frac{1}{\alpha} \cdot M \cdot\left(\frac{1}{2^{n} n !}\right)^{\frac{1}{2}} \alpha x \mathrm{H}_{n}(\alpha x)\\= & \frac{1}{\alpha} \cdot M \cdot\left(\frac{1}{2^{n} n !}\right)^{\frac{1}{2}}\left(\frac{1}{2} \mathrm{H}_{n+1}(\alpha x)+n \mathrm{H}_{n-1}(\alpha x)\right) \\= & \frac{1}{\alpha} M\left(\frac{1}{2^{n+1}(n+1) !}\right)^{\frac{1}{2}} \sqrt{\frac{n+1}{2}} \mathrm{H}_{n+1}(\alpha x)+\frac{1}{\alpha} M\left(\frac{1}{2^{n-1}(n-1) !}\right)^{\frac{1}{2}} \sqrt{\frac{n}{2}} \mathrm{H}_{n-1}(\alpha x) \\= & \frac{1}{\alpha}\left[\sqrt{\frac{n}{2}} \psi_{n-1}(x)+\sqrt{\frac{n+1}{2}} \psi_{n+1}(x)\right]\end{aligned}\]
其中 \(\displaystyle M=\sqrt{\alpha} \pi^{-\frac{1}{4}} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}}\);
利用本征函数的正交性:
\[\begin{aligned}\overline{x} & = \int \psi_{n}^{*} x \psi_{n} \mathrm{~d} x\\&=\int \psi_{n}^{*} \frac{1}{\alpha}\left[\sqrt{\frac{n}{2}} \psi_{n-1}(x)+\sqrt{\frac{n+1}{2}} \psi_{n+1}(x)\right]\mathrm{~d} x\\&=0\end{aligned}\]
我们可以得到 \(\overline{x}=0\)。
\[\begin{aligned}x^{2} \psi_{n}(x)= & \frac{1}{\alpha}\left[\sqrt{\frac{n}{2}} x \psi_{n-1}(x)+\sqrt{\frac{n+1}{2}} x \psi_{n+1}(x)\right] \\= & \frac{1}{\alpha}\left\{\sqrt{\frac{n}{2}} \cdot \frac{1}{\alpha}\left[\sqrt{\frac{n-1}{2}} \psi_{n-2}(x)+\sqrt{\frac{n}{2}} \psi_{n}(x)\right]\right. \left.+\sqrt{\frac{n+1}{2}} \cdot \frac{1}{\alpha}\left[\sqrt{\frac{n+1}{2}} \psi_{n}+\sqrt{\frac{n+2}{2}} \psi_{n+2}\right]\right\} \\= & \frac{1}{2 \alpha^{2}}\left[\sqrt{n(n-1)} \psi_{n-2}+(2 n+1) \psi_{n}+\sqrt{(n+1)(n+2)} \psi_{n+2}\right]\end{aligned}\]
同样,利用本征函数的正交归一性,我们可以得到:
\[\begin{array}{ll}\displaystyle \overline{V}&\displaystyle=\frac{1}{2} m \omega^{2} \int \psi_{n}^{*} x^{2} \psi_{n} \mathrm{~d} x\\&\displaystyle=\frac{1}{2} m \omega^{2} \int \psi_{n}^{*} \frac{1}{2 \alpha^{2}}\left[\sqrt{n(n-1)} \psi_{n-2}+(2 n+1) \psi_{n}+\sqrt{(n+1)(n+2)} \psi_{n+2}\right] \mathrm{~d} x\\&\displaystyle=\frac{1}{2} m \omega^{2} \frac{2 n+1}{2 \alpha^{2}}\\&\displaystyle=\frac{1}{2}\left(n+\frac{1}{2}\right) \hbar \omega\\&\displaystyle=\frac{E_{n}}{2}\end{array}\]
从上式,我们也可以得到:\(\displaystyle \overline{x^{2}}=\frac{2 n+1}{2 \alpha^{2}}\)
在 \(\psi_{n}\) 态下,\(\overline{x}=0\),\(\displaystyle \overline{x^{2}}=\frac{2 n+1}{2 \alpha^{2}}\),所以
\[\begin{aligned}\Delta x & = \sqrt{\overline{(x-\overline{x})^{2}}} \\&=\sqrt{\overline{\overline{x}^2-2x\overline{x}+x^2}}\\& = \sqrt{\overline{x^{2}}} \\& = \frac{1}{\alpha} \sqrt{\frac{2 n+1}{2}}\end{aligned}\]
利用
\[\begin{array}{c}\displaystyle\mathrm{H}_{n}^{\prime}(x)=2 n \mathrm{H}_{n-1}(x) \\\displaystyle\psi_{n}(x)=\left(\frac{\alpha}{\sqrt{\pi} 2^{n} n !}\right)^{\frac{1}{2}} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}} \mathrm{H}_{n}(\alpha x) \\\displaystyle\psi_{n-1}(x)=\left(\frac{\alpha}{\sqrt{\pi} 2^{n-1}(n-1) !}\right)^{\frac{1}{2}} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}} \mathrm{H}_{n-1}(\alpha x) \\\displaystyle\psi_{n+1}(x)=\left(\frac{\alpha}{\sqrt{\pi} 2^{n+1}(n+1) !}\right)^{\frac{1}{2}} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}} \mathrm{H}_{n+1}(\alpha x)\end{array}\]
所以
\[\begin{aligned}\frac{\mathrm{d}}{\mathrm{d} x} \psi_{n} & =\left(\frac{\alpha}{\sqrt{\pi} 2^{n} n !}\right)^{\frac{1}{2}} 2 n \alpha \mathrm{H}_{n-1} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}}-\alpha^{2} x \psi_{n} \\&=\left(\frac{\alpha}{\sqrt{\pi} 2^{n} n !}\right)^{\frac{1}{2}} 2 n \alpha \mathrm{H}_{n-1} \mathrm{e}^{-\frac{\alpha^{2} x^{2}}{2}}-\alpha^{2} \frac{1}{\alpha}\left[\sqrt{\frac{n}{2}} \psi_{n-1}(x)+\sqrt{\frac{n+1}{2}} \psi_{n+1}(x)\right] \\& =2 \alpha \sqrt{\frac{n}{2}} \psi_{n-1}-\alpha^{2} \frac{1}{\alpha}\left[\sqrt{\frac{n}{2}} \psi_{n-1}+\sqrt{\frac{n+1}{2}} \psi_{n+1}\right] \\& =\alpha\left[\sqrt{\frac{n}{2}} \psi_{n-1}-\sqrt{\frac{n+1}{2}} \psi_{n+1}\right]\end{aligned}\]
利用本征函数的正交归一性,我们可知:
\[\begin{aligned}\overline{p} & = -i\hbar\int \psi_{n}^{*} \frac{\mathrm{d}}{\mathrm{d}x} \psi_{n} \mathrm{~d} x\\&=-i\hbar\int \psi_{n}^{*} \alpha\left[\sqrt{\frac{n}{2}} \psi_{n-1}-\sqrt{\frac{n+1}{2}} \psi_{n+1}\right] \mathrm{d} x\\&=0\end{aligned}\]
另外,根据公式 $\displaystyle\frac{\mathrm{d}}{\mathrm{d} x} \psi_{n}(x)=\alpha\left[\sqrt{\frac{n}{2}} \psi_{n-1}-\sqrt{\frac{n+1}{2}} \psi_{n+1}\right] $,我们可以递推得到:
\[\begin{array}{ll}\displaystyle\frac{\mathrm{d}^{2}}{\mathrm{~d} x^{2}} \psi_{n}&\displaystyle=\alpha\left[\sqrt{\frac{n}{2}} \frac{\mathrm{d} \psi_{n-1}}{\mathrm{~d} x}-\sqrt{\frac{n+1}{2}} \frac{\mathrm{d} \psi_{n+1}}{\mathrm{~d} x}\right] \\&\displaystyle=\alpha\left\{\sqrt{\frac{n}{2}} \alpha\left[\sqrt{\frac{n-1}{2}} \psi_{n-2}-\sqrt{\frac{n}{2}} \psi_{n}\right]-\sqrt{\frac{n+1}{2}} \alpha\left[\sqrt{\frac{n+1}{2}} \psi_{n}-\sqrt{\frac{n+2}{2}} \psi_{n+2}\right]\right\} \\&\displaystyle=\frac{\alpha^{2}}{2}\left[\sqrt{n(n-1)} \psi_{n-2}-(2 n+1) \psi_{n}+\sqrt{(n+1)(n+2)} \psi_{n+2}\right]\end{array}\]
类似的,利用本征函数的正交归一性,我们可以得到:
\[\begin{aligned}\overline{p^{2}} & = \int_{-\infty}^{+\infty} \psi_{n}^{*}\left(-\hbar^{2} \frac{\partial^{2}}{\partial x^{2}}\right) \psi_{n} \mathrm{~d} x \\& = -\hbar^{2}\int_{-\infty}^{+\infty} \psi_{n}^{*}\frac{\alpha^{2}}{2}\left[\sqrt{n(n-1)} \psi_{n-2}-(2 n+1) \psi_{n}+\sqrt{(n+1)(n+2)} \psi_{n+2}\right] \mathrm{~d} x \\& = \frac{\hbar^{2} \alpha^{2}}{2}(2 n+1)\\\end{aligned}\]
所以
\[\displaystyle \overline{T}=\frac{\overline{p^{2}}}{2 m}=\frac{1}{2}\left(n+\frac{1}{2}\right) \hbar \omega=\frac{E_{n}}{2}\]
在 \(\psi_{n}\) 态下,\(\overline{p}=0\),\(\displaystyle \overline{p^{2}}=\frac{\alpha^{2} \hbar^{2}}{2}(2 n+1)\),所以
\[\begin{aligned}\Delta p & =\sqrt{\overline{(p-\overline{p})^{2}}} \\& = \sqrt{\overline{p^2-2p\overline{p}+\overline{p}^2}} \\& = \sqrt{\overline{p^2}} \\& = \alpha \hbar \sqrt{\frac{2 n+1}{2}}\end{aligned}\]
因此,我们可以得到:
\[\displaystyle \Delta x \Delta p=\frac{1}{\alpha} \sqrt{\frac{2 n+1}{2}}\times \alpha \hbar \sqrt{\frac{2 n+1}{2}}=(n+\frac{1}{2}) \hbar\]
符合不确定系关系:\(\displaystyle \Delta x \Delta p \geq \frac{\hbar}{2}\)
在实验上,我们曾经对 \(\Delta x\) 进行过测量:

图片链接
因为 \(\displaystyle \alpha=\sqrt{\frac{\mu \omega_{0}}{\hbar}}\) 和 \(\displaystyle \Delta x = \frac{1}{\alpha} \sqrt{\frac{2 n+1}{2}}\),所以在 \(n=0\) 的时候,\(\Delta x\) 的表现形式为:
\[\displaystyle \Delta x_{\mathrm{SQL}}=\sqrt{\frac{\hbar}{2 \mu \omega_{0}}}\]
我们称其为标准量子极限(standard quantum limit)。
在同时考虑了谐振器和线性放大器的量子噪声,我们可以得到:
\[\displaystyle \Delta x_{\mathrm{QL}}=\sqrt{\frac{\hbar}{\ln 3 \cdot \mu \omega_{0}}} \approx 1.35 \cdot \Delta x_{\mathrm{SQL}}\]
当 \(\mathrm{V}_{\mathrm{NR}}=15 \mathrm{~V}\) 时,我们发现我们的位移传感方案在机械共振时的噪声温度为:
\[T_{N}^{S S E T}=16 m K=17 \hbar \omega_{0}=18 T_{Q L}\]
由此,我们可以给出位置标准偏差:
\[\displaystyle \Delta x=\sqrt{\frac{T_{N}^{S S E T}}{T_{Q L}}} \cdot \Delta x_{Q L}=4.3 \cdot \Delta x_{Q L}\]

图片链接
通过进行实验测量,我们发现实验值与理论值符合的很好。






