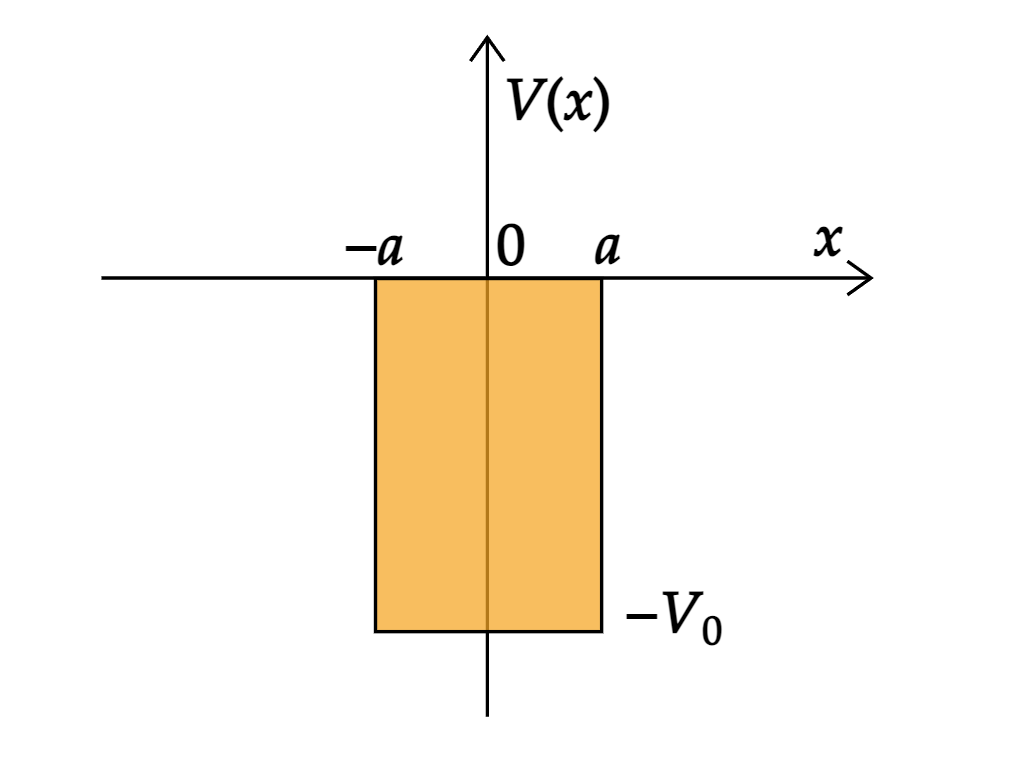一维有限深势阱
一个质量为 \(\mu\) 的粒子在一维势场 \(V(x)=\left\{\begin{array}{ll}0, & |x|>a \\-V_{0}, & |x|<a\end{array}\right.\) 中运动，其中 \(V_{0}>0\) 。
- 求基态能量 \(E_0\) 满足的方程；
- 求存在且仅存在一个束缚态的条件；
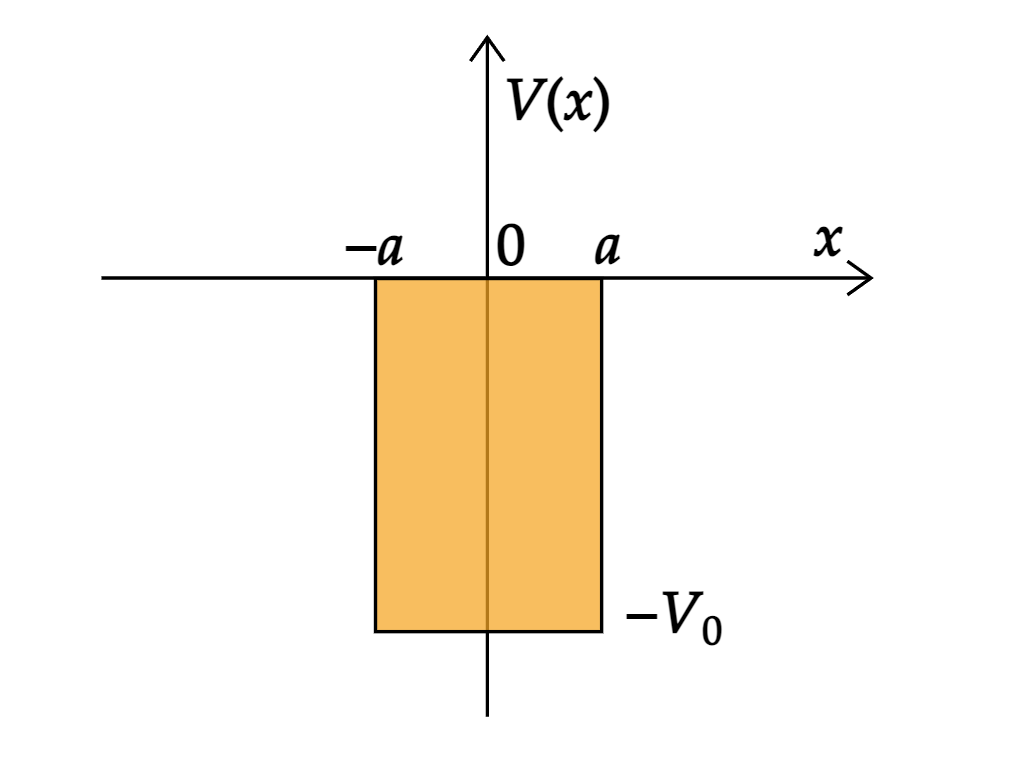图1：一维有限深势阱
解：
在此势场中的定态方程为：
\[
\begin{equation}
\begin{array}{ll}
\displaystyle-\frac{\hbar^{2}}{2 \mu} \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}}=E \psi(x), & |x|>a \\
\displaystyle-\frac{\hbar^{2}}{2 \mu} \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}}-V_{0} \psi(x)=E \psi(x), & |x|<a\end{array}
\end{equation}
\]
束缚态：粒子只能在一定范围内运动，不能运动到无穷远处。
在此势场中，要形成束缚态，能量 \(E\) 只能在 0 与 \(-V_0\) 之间，即 \(-V_0<E<0\)。
令
\[
\begin{align}E & = -|E|\\\alpha & = \sqrt{\frac{2 \mu|E|}{\hbar^{2}}}\\\beta & = \sqrt{\frac{2 \mu\left(V_{0}-|E|\right)}{\hbar^{2}}}\end{align}
\]
定态方程变为：
\[
\begin{equation}
\begin{array}{l}\displaystyle \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}}=\alpha^{2} \psi(x), &|x|>a \\\displaystyle\frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}}=-\beta^{2} \psi(x),&|x|<a\end{array}
\end{equation}
\]
二阶常系数齐次线性微分方程：
\[
\begin{equation}
y^{\prime \prime}+p y^{\prime}+q y=0
\end{equation}
\]
根据之前的文章“二阶线性微分方程|1”，我们可以知道：
- 当常系数是 \(\alpha^2\) 时，通解形式：\(y=C_1 e^{\alpha x}+C_2 e^{-\alpha x}\)
- 当常系数是 \(-\beta^2\) 时，通解形式：\(y=C_3 \cos \beta x+C_4 \sin \beta x\)（因为 \(\alpha=0\)）
在一维情况下，当势能是对称的时候，波函数束缚态的解只有两种情况：偶宇称、奇宇称
偶宇称
通过薛定谔方程，波函数的解为：
\[
\begin{equation}
\begin{array}{lc}
\psi_{1}(x)=C_1 \mathrm{e}^{\alpha x}+C_2 e^{-\alpha x},& x\le -a \\
\psi_{2}(x)=C_3 \cos \beta x+C_4 \sin \beta x,&-a<x<a \\
\psi_{3}(x)=C_1 \mathrm{e}^{\alpha x}+C_2 e^{-\alpha x}, & x\ge a
\end{array}
\end{equation}
\]
因为 \(|\psi_i(x)|^2\) 是粒子在该处的概率，概率不能无穷大。
并且 \(V(x)\) 满足对称条件 \(V(-x)=V(x)\) ，一维束缚定态有确定的偶宇称。
所以公式（7）可以变换为：
\[
\begin{equation}
\begin{array}{lc}
\psi_{1}(x)=A \mathrm{e}^{\alpha x},& x\le -a \\
\psi_{2}(x)=B \cos \beta x,&-a<x<a \\
\psi_{3}(x)=A \mathrm{e}^{-\alpha x}, & x\ge a
\end{array}
\end{equation}
\]
注：\(A\) 和 \(B\) 只是归一化系数。
根据 \(\psi\) 与 \(\psi'\) 在 \(x=a\) 点的连续条件，我们可以得到：
\[
\begin{align}B \cos \beta a & = A \mathrm{e}^{-\alpha a} \\B \beta \sin \beta a & = A \alpha \mathrm{e}^{-\alpha a}\end{align}
\]
将以上两式相比，可以得到：
\[
\begin{align}\beta \tan \beta a & = \alpha\end{align}
\]
令 \(\eta=\alpha a\) ，\(\zeta=\beta a\)，公式（11）变为：
\[
\begin{equation}
\eta=\zeta \tan \zeta
\end{equation}
\]
根据 \(\eta=\alpha a\) ，\(\zeta=\beta a\) 、公式（2）、公式（3）和公式（4），我们可以得到：
\[
\begin{align}
\eta^{2}+\zeta^{2} & = \frac{2 \mu V_{0} a^{2}}{\hbar^{2}} \equiv Q^{2} \text { (常数) }
\\ Q & = \sqrt{\frac{2 \mu V_{0} a^{2}}{\hbar^{2}}}
\end{align}
\]
偶宇称定态能量由公式（12）与公式（13）通过作图法确定。
因为 \(\alpha>0\)，\(\beta>0\)，所以 \(\eta>0\)，\(\eta>0\)。
如下图所示，由曲线 \(\eta=\zeta \tan \zeta\) 与半径为 \(Q\) 的圆在 \((\eta, \zeta)\) 坐标系的第一象限 \((\eta>0, \zeta>0)\) 内的交点得到 \(\eta_{0}, \eta_{2}, \cdots, \eta_{i}, \cdots\)，从而得到偶宇称定态能量：
\[
\begin{equation}
E_{i}=-\frac{\eta_{i}^{2} \hbar^{2}}{2 \mu a^{2}}, i=0,2, \cdots
\end{equation}
\]
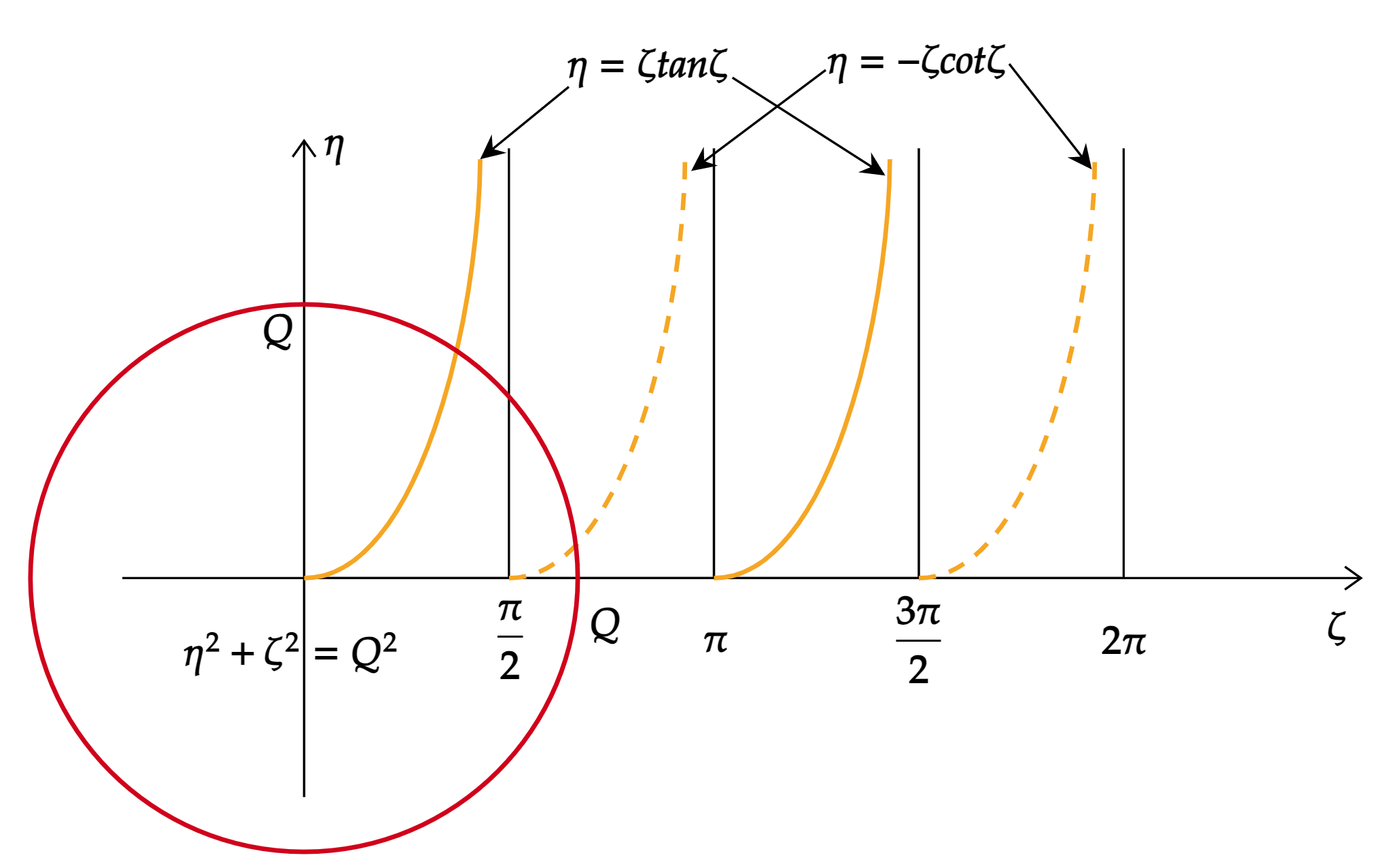图2：一维有限深势阱的解
从上图中可以看出，无论势阱参数 \(V_0\) 与 \(a\) 取什么值，至少存在一个偶宇称束缚态——基态。
基态能量 \(E_0\) 满足公式（12）和公式（13）。
奇宇称
通过薛定谔方程，波函数的解为：
\[
\begin{equation}
\begin{array}{lc}
\psi_{1}(x)=C_1 \mathrm{e}^{\alpha x}+C_2 e^{-\alpha x},& x\le -a \\
\psi_{2}(x)=C_3 \cos \beta x+C_4 \sin \beta x,&-a<x<a \\
\psi_{3}(x)=C_1 \mathrm{e}^{\alpha x}+C_2 e^{-\alpha x}, & x\ge a
\end{array}
\end{equation}
\]
因为 \(|\psi_i(x)|^2\) 是粒子在该处的概率，概率不能无穷大。
并且 \(V(x)\) 满足对称条件 \(V(-x)=-V(x)\) ，一维束缚定态有确定的宇称。
方程（16）的奇宇称解为：
\[
\begin{equation}
\begin{array}{lc}
\psi_{1}(x)=-A \mathrm{e}^{\alpha x},& x\le -a \\
\psi_{2}(x)=B \sin \beta x,&-a<x<a \\
\psi_{3}(x)=A \mathrm{e}^{-\alpha x}, & x\ge a
\end{array}
\end{equation}
\]
根据 \(\psi\) 与 \(\psi'\) 在 \(x=-a\) 点的连续条件，我们可以得到：
\[
\begin{align}
B \sin \beta a & = A \mathrm{e}^{-\alpha a} \\
B \beta \cos \beta a & = A \alpha \mathrm{e}^{-\alpha a}
\end{align}
\]
类似的推导可得奇宇称态能量由下属公式：
\[
\begin{equation}
\eta=-\zeta \cot \zeta
\end{equation}
\]
和
\[
\begin{align}
\eta^{2}+\zeta^{2} & = \frac{2 \mu V_{0} a^{2}}{\hbar^{2}} \equiv Q^{2} \text { (常数) }
\\ Q & = \sqrt{\frac{2 \mu V_{0} a^{2}}{\hbar^{2}}}
\end{align}
\]
决定。
从上图中可以看出，只有当 \(\displaystyle Q>\frac{\pi}{2}\) 时，才存在奇宇称束缚态（两条曲线才有交点）。
奇宇称态的最低能量 \(E_{1}>E_{0}\) ，为体系的第一激发态能量。
由此可见，体系存在且仅存在一个束缚态的条件为：
\[
\begin{equation}
Q=\sqrt{\frac{2 \mu V_{0} a^{2}}{\hbar^{2}}}<\frac{\pi}{2} \quad \text { 或 } \quad V_{0} a^{2}<\frac{\pi^{2} \hbar^{2}}{8 \mu}
\end{equation}
\]