VASP中的磁性设置

背景知识

在居里温度一下，铁磁，反铁磁，亚铁磁都是磁有序的。

当温度超过居里温度的时候，材料会从磁有序变为磁无序。

图1

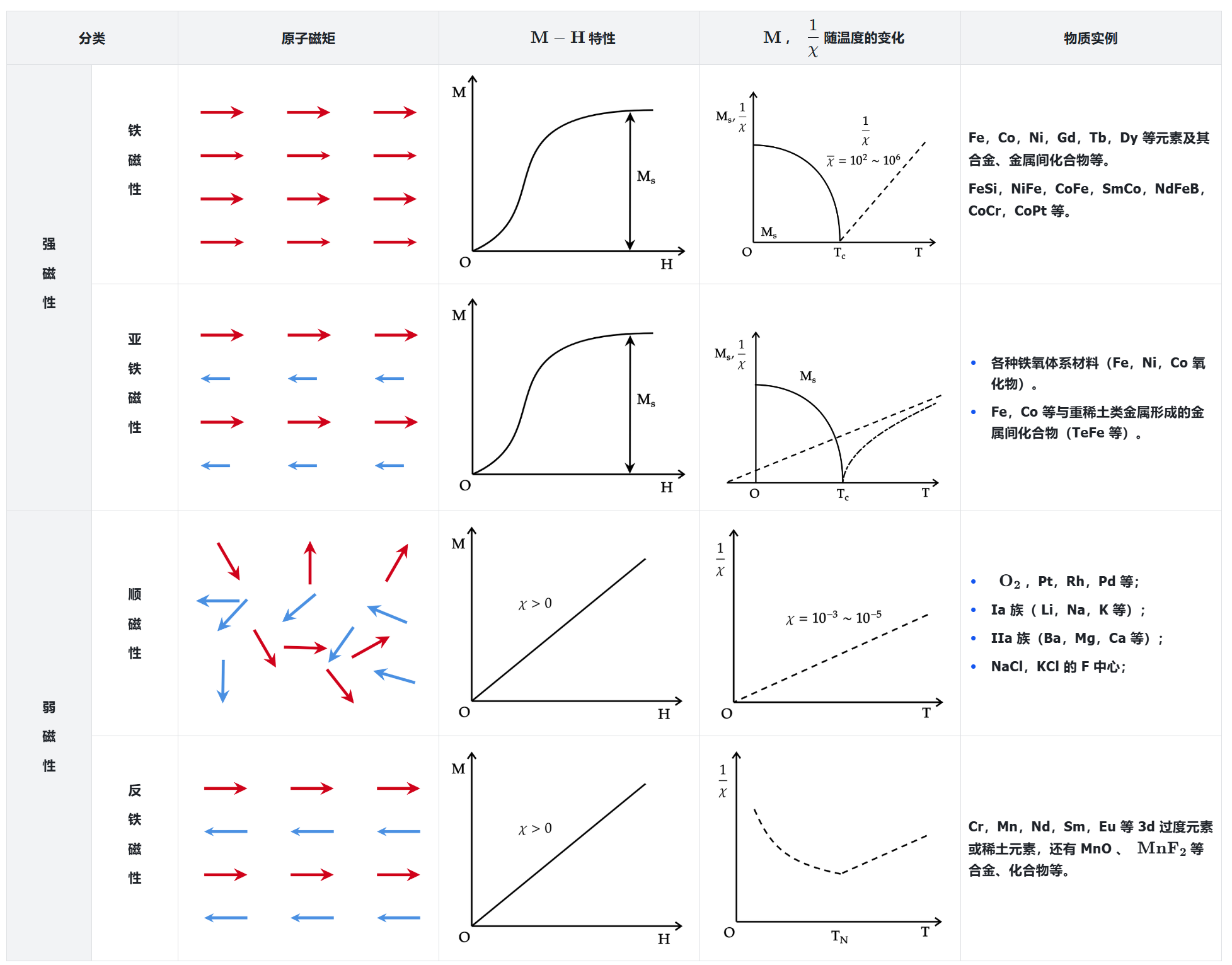
其中，铁磁和亚铁磁都有净磁矩，反铁磁和顺磁材料没有净磁矩。

铁磁性： 在没有施加磁场的情况下，铁磁材料中的磁矩有序且具有相同的大小。

亚铁磁性： 这是在没有施加磁场的情况下，亚铁磁材料中的磁矩是由两种不同的离子组成，并且磁矩相反对齐并且具有不同的大小。

顺磁性： 在没有施加磁场的情况下，顺磁材料中的磁矩是无序的，并且在施加的磁场的情况下变为有序。

反铁磁性： 没有施加磁场的情况下，反铁磁材料中的磁矩是相反的，并且具有相同的大小，所以总磁矩为零。

居里温度（Curie temperature）： 指磁性材料中自发磁化强度降到零时的温度，是物质由铁磁性或亚铁磁性转变成顺磁性的临界点，记为 \(T_C\)。低于居里温度时，该物质含有磁性，此时和材料有关的磁场很难改变。高于居里温度时，该物质成为顺磁体，此时磁体的磁场很容易随周围磁场的改变而改变。居里温度由物质的化学成分和晶体结构决定。

奈尔温度（Néel temperature）： 指的是反铁磁性材料转变为顺磁性材料所需要达到的温度，记为 \(T_N\)。当温度升到奈尔温度时，晶体内部的原子内能会大到足以破坏材料内部宏观磁性排列，从而发生相变，物质由反铁磁性转变为顺磁性。

居里定律： 在顺磁性材料中，材料的磁化强度大致与施加的磁场强度成正比。然而，若加热材料，则比值减小。对于固定场强的磁场，磁化率大致与温度成反比。

\[ \mathbf{M}=C\cdot \frac{\mathbf{B}}{T} \]

\(\mathbf{M}\)：磁化强度； \(\mathbf{B}\)：磁感应强度； \(T\)：绝对温度，单位为 \(K\)； \(C\)：居里常数；

居里-韦斯定律（Curie-Weiss law）： 居里-韦斯定律为居里定律的修正公式，用来补足该公式的不足。当一物质的温度大于居里温度（\(T_C\)）时，其磁化率 \(\chi\) 与温度 \(T\) 的关系式为：

\[ \chi=\frac{C}{T-T_C} \]

\(C\)：居里常数； \(T\)：绝对温度，单位为 \(K\)； \(T_C\)：居里温度，单位为 \(K\)；

磁性的设置

在 VASP 中进行磁性材料计算之前，我们需要在 INCAR 中设置相关的磁性参数。

对于简单的磁性材料，我们只需要在 INCAR 中设置 ISPIN=2，不需要设置 MAGMOM。

对于复杂的磁性体系，我们除了需要在 INCAR 中设置 ISPIN=2，还需要设置 MAGMOM。

MAGMOM 可以指定体系中原子的初始磁矩。

合理的初始值可以加快计算速度，并保持计算结果的正确性。

MAGMOM 写入参数最简单的方式就是对照 POSCAR 中原子的顺序，依次在 MAGMOM 中写入磁矩：

Text Only

MAGMOM = m1 m2 m3 m4 ...

也可以在磁矩前面加上数字：

Text Only

MAGMOM = n*m

上述代表有 n 个原子的磁矩都是 m。

对于包含许多原子的系统，单行上的 MAGMOM 输入可能很难读取，特别是在非共线的情况下。可以使用反斜杠（\）作为换行符在多行上提供 INCAR 输入。例如，对于具有 AFM 排列和 16 个原子（其中前 8 个是磁性的）的非共线系统，多线输入可能如下：

Text Only

MAGMOM =  3.0  2.0  1.0 \
         -3.0 -2.0 -1.0 \
          3.0  2.0  1.0 \
         -3.0 -2.0 -1.0 \
          3.0  2.0  1.0 \
         -3.0 -2.0 -1.0 \
          3.0  2.0  1.0 \
         -3.0 -2.0 -1.0 \
          24*0.0

注：当只设置 ISPIN=2 的时候，体系的每个原子都默认加上磁矩 1。

注：为了收敛到磁基态，建议将磁矩设置为略大于预期值，例如，使用实验磁矩乘以 1.2 或 1.5。

注：最终的磁性状态在很大程度上取决于 MAGMOM 的初始值。即使没有使用对称性（ISYM=-1），结果也是这样，因为大多数交换相关泛函在自旋密度泛函理论中都有许多局部最小值。

氧原子

\(\rm O_2\) 分子中有 12 个价电子。¹

以 x 轴作为键轴，两个氧原子的一对 \(2s\) 轨道组合得到氧分子的成键轨道 \(\sigma_{2 s}\) 和反键轨道 \(\sigma_{2 s}^*\)；

两个 \(2p_x\) 原子轨道“头碰头”组合得到 \(\sigma_{2 p_{x}}\) 和 \(\sigma_{2 p_{x}}^*\)；

两个 \(2p_y\) 和两个 \(2p_z\) 轨道分别组合，得到两个简并的成键轨道（\(\pi_{2 p_{y}}\) 和 \(\pi_{2 p_{z}}\)）和两个简并的反键轨道(\(\pi_{2 p_{y}}^*\) 和 \(\pi_{2 p_{z}}^*\))。

图2

图片链接

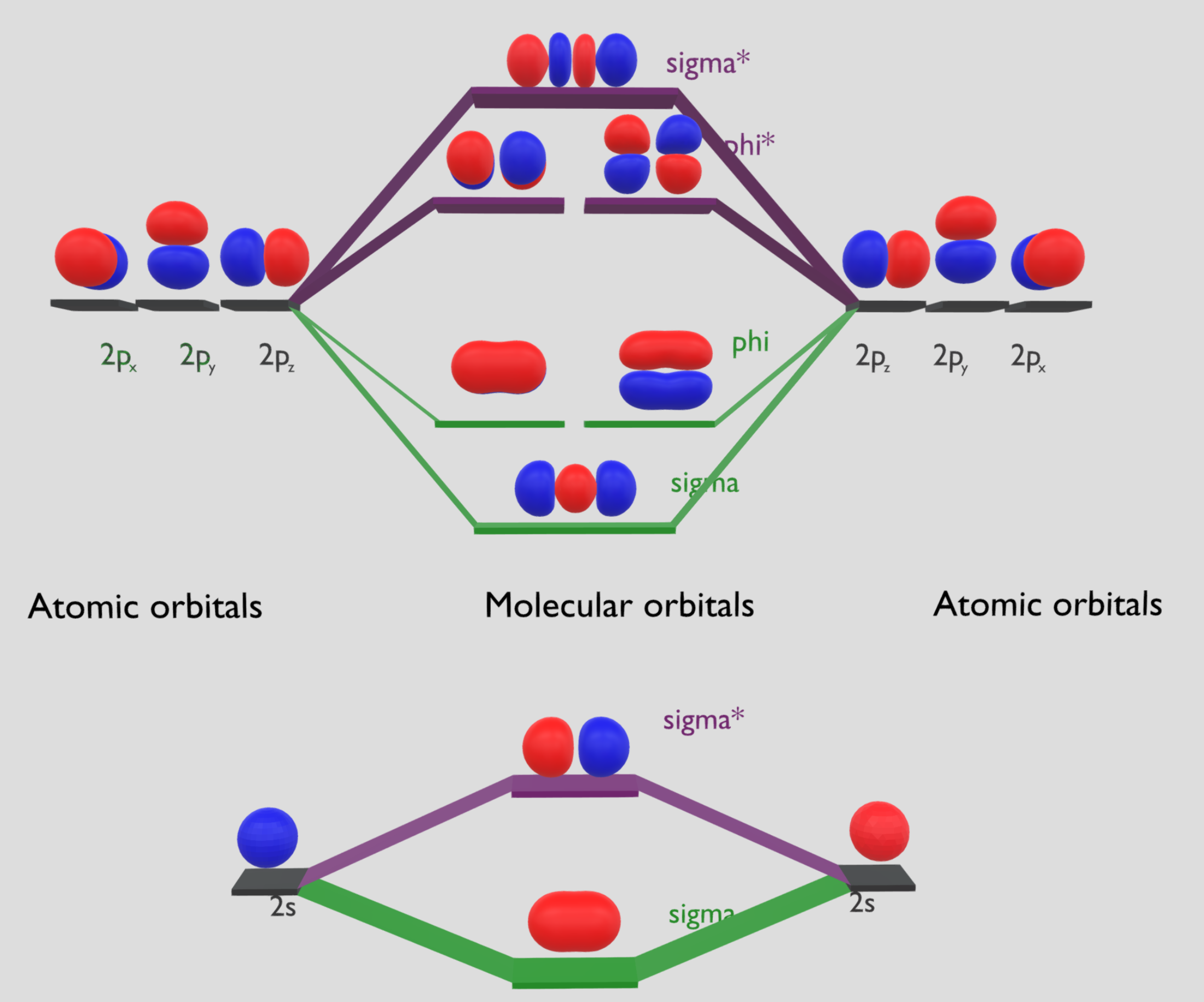
\(O_2\) 电子组态的表示方法：\(\left(\sigma_{1 s}\right)^{2}\left(\sigma_{1 s}^{*}\right)^{2}\left(\sigma_{2 s}\right)^{2}\left(\sigma_{2 s}{ }^{*}\right)^{2}\left(\sigma_{2 p}\right)^{2}\left(\pi_{2 p}\right)^{4}\left(\pi_{2 p}{ }^{*}\right)^{2}\)

\(\pi_{2 p_{y}}^*\) 和 \(\pi_{2 p_{z}}^*\) 中填充了两个单电子，根据洪特规则，这两个电子应自旋平行地排列在两个简并轨道中，从而成功解释了 \(\rm O_2\) 的顺磁性。

图3

图片链接

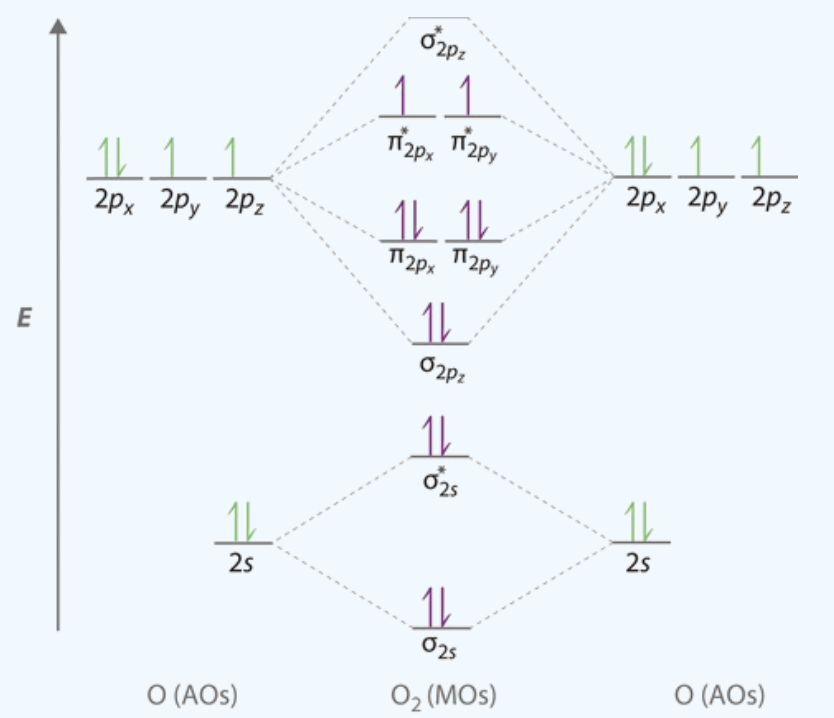
通过上图可以知道：\(\rm O_2\) 分子的基态是三重态，也就是每个原子都有一点单电子，所以每个氧原子的初始的磁矩可以设置为 1。

但 VASP 对 MAGMOM 的要求不一定非得是 1，也就是初始值是一个可以模糊也可以精确的数值。因为很多时候，我们不知道确切的磁矩是多少。如果我们已经知道磁矩是多少（比如 \(\rm O_2\) ），可以直接写上去，也可以差不多写一个。如果不知道的话，就需要根据自己的假设，猜一个初始值了。²

输入文件

INCAR、POTCAR 和 KPOINTS 是通过 vaspkit 生成。

INCAR

INCAR 参数在 vaspkit 生成的基础上，添加了相关的磁性参数。

Text Only

Global Parameters
ISTART =  1            (Read existing wavefunction, if there)
ISPIN  =  2            (Non-Spin polarised DFT)
MAGMOM =  1.5 1.5 1.5 1.5
# ICHARG =  11         (Non-self-consistent: GGA/LDA band structures)
LREAL  = .FALSE.       (Projection operators: automatic)
# ENCUT  =  400        (Cut-off energy for plane wave basis set, in eV)
# PREC   =  Accurate   (Precision level: Normal or Accurate, set Accurate when perform structure lattice relaxation calculation)
LWAVE  = .TRUE.        (Write WAVECAR or not)
LCHARG = .TRUE.        (Write CHGCAR or not)
ADDGRID= .TRUE.        (Increase grid, helps GGA convergence)
# LVTOT  = .TRUE.      (Write total electrostatic potential into LOCPOT or not)
# LVHAR  = .TRUE.      (Write ionic + Hartree electrostatic potential into LOCPOT or not)
# NELECT =             (No. of electrons: charged cells, be careful)
# LPLANE = .TRUE.      (Real space distribution, supercells)
# NWRITE = 2           (Medium-level output)
# KPAR   = 2           (Divides k-grid into separate groups)
# NGXF    = 300        (FFT grid mesh density for nice charge/potential plots)
# NGYF    = 300        (FFT grid mesh density for nice charge/potential plots)
# NGZF    = 300        (FFT grid mesh density for nice charge/potential plots)

Static Calculation
ISMEAR =  0            (gaussian smearing method)
SIGMA  =  0.05         (please check the width of the smearing)
LORBIT =  11           (PAW radii for projected DOS)
NEDOS  =  2001         (DOSCAR points)
NELM   =  60           (Max electronic SCF steps)
EDIFF  =  1E-08        (SCF energy convergence, in eV)

KPOINTS

Text Only

K-Spacing Value to Generate K-Mesh: 0.020
0
Gamma
  10  15  14
0.0  0.0  0.0

POSCAR

Text Only

O4
1.0
   0.0000000000000000    5.7028057065333089    0.0000000000000000
   3.3248318800000001    0.0000000000000000    0.0000000000000000
   0.0000000000000000   -2.3944914034358917   -3.6470501823735777
O
4
direct
   0.9745461700000000    0.0000000000000000    0.8444259800000000 O
   0.5254538300000000    0.5000000000000000    0.1555740200000000 O
   0.4745461700000000    0.5000000000000000    0.8444259800000000 O
   0.0254538300000000    0.0000000000000000    0.1555740200000000 O

计算结果

OUTCAR 文件中有关磁性的输出结果：

Text Only

# of ion       s       p       d       tot
------------------------------------------
    1        0.010   0.803   0.000   0.814
    2        0.010   0.803   0.000   0.814
    3        0.010   0.803   0.000   0.814
    4        0.010   0.803   0.000   0.814
--------------------------------------------------
tot          0.042   3.213   0.000   3.255

OUTCAR 文件中有关计算时间的输出结果：

Text Only

 General timing and accounting informations for this job:
 ========================================================

                  Total CPU time used (sec):      624.047
                            User time (sec):      613.420
                          System time (sec):       10.627
                         Elapsed time (sec):      629.221

讨论

在 VASP 的官方手册中，有这样一句话：³

If you have problems converging to a desired magnetic solution, try to calculate first the non-magnetic ground state and continue from the generated WAVECAR and CHGCAR.

我们根据这一句话，先进行非磁性的基态计算，求出 WAVECAR 和 CHGCAR。然后再磁性基态计算的时候读取 WAVECAR 和 CHGCAR 文件。

读取 WAVECAR 和 CHGCAR 文件后，OUTCAR 文件中有关磁性的输出结果为：

Text Only

# of ion       s       p       d       tot
------------------------------------------
    1        0.010   0.803   0.000   0.814
    2        0.010   0.803   0.000   0.814
    3        0.010   0.803   0.000   0.814
    4        0.010   0.803   0.000   0.814
--------------------------------------------------
tot          0.042   3.213   0.000   3.255

读取 WAVECAR 和 CHGCAR 文件后，OUTCAR 文件中有关计算时间的输出结果为：

Text Only

 General timing and accounting informations for this job:
 ========================================================

                  Total CPU time used (sec):      476.579
                            User time (sec):      466.093
                          System time (sec):       10.486
                         Elapsed time (sec):      487.039

磁矩的收敛结果一样。

和 629.221 秒相比，计算时间有了很大的提升。

但是，这只是表象。

进行非磁性计算所需要的时间为：

Text Only

 General timing and accounting informations for this job:
 ========================================================

                  Total CPU time used (sec):      277.846
                            User time (sec):      271.680
                          System time (sec):        6.166
                         Elapsed time (sec):      283.972

所以，这样计算所花费的总时间为 771.011 秒。

和 629.221 秒相比，多出来了 22.5% 的时间。

结论：非磁性计算可以降低磁性计算的时间，但是计算的总时间会增加。

---

1. https://www.dxhx.pku.edu.cn/article/2023/1000-8438/20230548.shtml ↩

2. https://www.bigbrosci.com/2017/12/04/ex12/ ↩

3. https://www.vasp.at/wiki/index.php/MAGMOM ↩

评论