一维无限深势阱¶

当粒子受到保守力场的限制，只能在一定范围内运动时，其势能曲线呈现出类似陷阱的形状，因此我们称之为“势阱”。

例如，电子在金属中的运动、质子在原子核中的势能曲线等都可以用这个概念来描述。

为了简化计算，我们引入一个理想的势阱模型——一维无限深势阱。

在这个模型中，粒子被限制在一个无限深的势能阱中，只能在有限的空间范围内运动。

设一维无限深势阱的势能分布如下：

\[U(x)=\left\{\begin{array}{ll}0 & 0<x<a \text { (阱内) } \\\infty & x \leq 0, x \geq a \text { (阱外) }\end{array}\right.\]

按照经典理论，处于无限深势阱中的粒子，其能量可取任意的有限值，粒子在宽度为 \(a\) 的势阱内各处的概率是相等的。

但从量子力学来看，这些问题又当如何呢？

下面我们应用薛定谔方程来讨论处于一维无限深势阱中粒子的运动。

由于势能不显含时间，需由定态薛定谔方程求解 \(\psi(x)\)，考虑到势能是分段的，列方程求解也需分阱外、阱内两个区间进行。

在阱外，设波函数为 \(\psi_e\)，定态薛定谔方程为：\(\displaystyle-\frac{\hbar}{2 m} \frac{\mathrm{d}^{2} \psi_{\mathrm{e}}}{\mathrm{d} x^{2}}+(E-U) \psi_{\mathrm{e}}=0\)

由于 \(U \rightarrow \infty\)，对于 \(E\) 为有限值的粒子，要使上述方程成立，唯有 \(\psi_e=0\)。

在阱内，设波函数为 \(\psi_i\)，定态薛定谔方程为：\(\displaystyle-\frac{\hbar^{2}}{2 m} \frac{\mathrm{d}^{2} \psi_{\mathrm{i}}}{\mathrm{d} x^{2}}=E \psi_{\mathrm{i}}\)

令 \(\displaystyle k^{2}=\frac{2 m E}{\hbar^{2}}\)，于是方程可改写为：\(\displaystyle\frac{\mathrm{d}^{2} \psi_{\mathrm{i}}}{\mathrm{d} x^{2}}+k^{2} \psi_{\mathrm{i}}=0\)

其解为：\(\psi_{\mathrm{i}}(x)=C \sin (k x+\delta)\)

式中 \(C\) 和 \(\delta\) 是两待定常数。

因为在阱壁上波函数必须单值、连续，即应有：

\[ \begin{array}{ll}\psi_{\mathrm{i}}(0)=\psi_{\mathrm{e}}(0)=0\\\psi_{\mathrm{i}}(a)=\psi_{\mathrm{e}}(a)=0\end{array} \]

由此得到：

\(\psi_{\mathrm{i}}(0)=C \sin \delta=0\)，及 \(\delta=0\)。

\(\psi_{\mathrm{i}}(a)=C \sin k a=0\)，及 \(k a=n \pi, n=1,2,3, \cdots\)。

对波函数归一化，我们可以得到：

\[\displaystyle\int_{0}^{a}|\Psi(x, t)|^{2} \mathrm{~d} x=\int_{0}^{a}|\psi(x)|^{2} \mathrm{~d} x=\int_{0}^{a}\left[C \sin \frac{n \pi x}{a}\right]^{2} \mathrm{~d} x=|C|^2\frac{a}{2}=1\]

最后得到归一化系数：\(\displaystyle C=\sqrt{\frac{2}{a}}\)

于是得定态波函数：\(\left\{\begin{array}{l}\displaystyle\psi_{\mathrm{e}}(x)=0 \\\displaystyle\psi_{\mathrm{i}}(x)=\sqrt{\frac{2}{a}} \sin \frac{n \pi}{a} x, n=1,2,3, \cdots\end{array}\right.\)

严格的来说，\(C\) 可以是复数，解为：\(\displaystyle C=\sqrt{\frac{2}{a}}e^{i\theta}\)

最后得波函数：\(\left\{\begin{array}{l}\displaystyle\Psi_{\mathrm{e}}(x, t)=0 \\\displaystyle\Psi_{\mathrm{i}}(x, t)=\sqrt{\frac{2}{a}} \sin (\frac{n \pi}{a} x) e^{\displaystyle-\frac{\mathrm{i}}{k}E t}\end{array}\right.\)

我们将一维无限深势阱中粒子运动的特征总结如下：

（1）粒子的能量不能连续地取任意值，只能取分立值。

因为 \(\displaystyle k^{2}=\frac{2 m E}{\hbar^{2}}\)\(，而\)\(\displaystyle k=\frac{n \pi}{a}\)。

所以 \(\displaystyle E=\frac{\hbar^{2} k^{2}}{2 m}=\frac{n^{2} \pi^{2} \hbar^{2}}{2 m a^{2}}=E_{n}\)，\(n=1,2,3, \cdots\)；

根据上式，我们发现能量是量子化的。

整数 \(n\) 被称为粒子能量的量子数。

图片链接

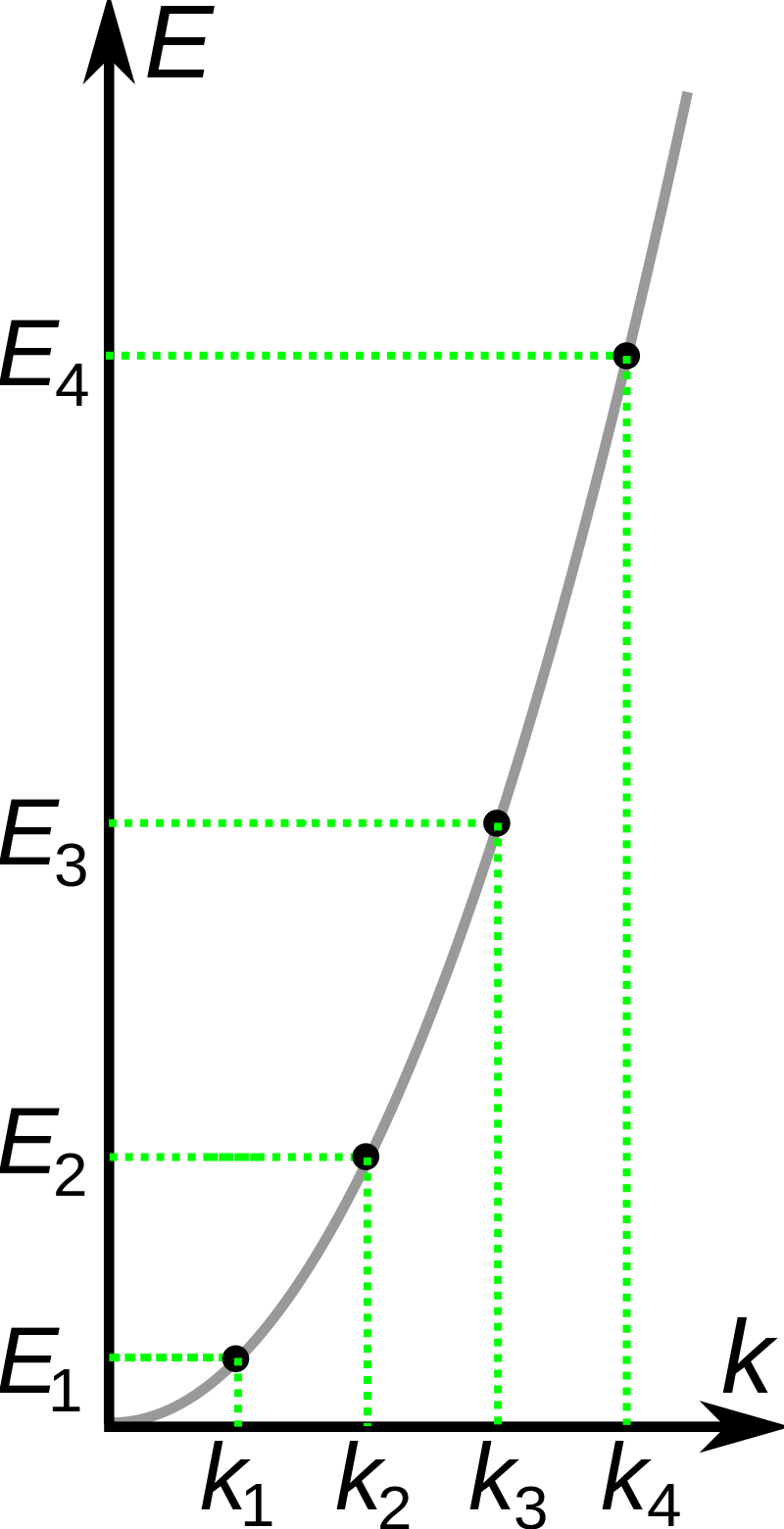
可见，能量量子化在量子力学中是很自然地得出的结果，并不求助于人为的假设。

粒子的能级：

图片链接

很重要的一点是，虽然表达粒子量子态的能量本征函数，其能量只能是离散能级谱中的一个能级。

这并不能防止粒子拥有任意的能量，只要这能量大于零点能量。

根据态叠加原理，粒子的量子态，可以是几个能量本征函数的叠加。

当测量粒子的能量时，测量的答案，只可能是叠加的几个能级中的一个能级。

由于测量会造成波函数坍缩，不能对同一个粒子做多次的测量，而指望得到有意义的答案。

必须假设准备了许多同样的系统。

对每一个系统内的粒子，做同样的测量。

虽然，每一次的测量的答案，只可能是叠加的几个能级中的一个能级。

所有答案的的平均值，是粒子的能量期望值。

（2）方势阱中的能级分布是不均匀的。

根据能级公式 \(\displaystyle E_n=\frac{n^{2} \pi^{2} \hbar^{2}}{2 m a^{2}}\)，我们可以得到相邻能级的差：

\[\displaystyle E_{n}-E_{n-1}=\frac{\hbar^{2}}{2 m a^{2}}[n^2-(n-1)^2]=\frac{(2n-1)\hbar^{2}}{2 m a^{2}}\]

随着能级的升高，相邻能级的能量间隙越来越大。

（3）粒子的最小能量不等于零。

因为 \(n=0\)，\(\Psi_{\mathrm{i}}(x, t)=0\)，说明不存在这种状态。

所以 \(n\) 最小取 1 ，粒子的最小能量：\(\displaystyle E_{1}=\frac{ \hbar^{2}}{2 m a^{2}}\)

粒子的最小能量状态称为基态，最小能量称为基态能。

上式表明，\(a\) 愈小，\(E_1\) 就愈大，粒子运动愈剧烈。

按照经典理论，粒子的能量是连续分布的，其能量可以为零。

但若能量为零，则动量必须为零，于是动量的不确定度 \(\Delta p\) 就不存在，根据不确定度关系 \(\displaystyle\Delta x \Delta p \geq \frac{\hbar}{2}\)，这只有 \(\Delta x \rightarrow \infty\) 才有可能。

实际上，粒子处于势阱中，它的 \(\Delta x\) 为势阱的宽度 \(a\) 所限制，从而导致最小能量的出现。

这种最小能量有时称为零点能。

所以，零点能的存在与不确定度关系是协调一致的。

许多实验证实了微观领域中能量量子化的分布规律，并证实了零点能的存在。

图片链接

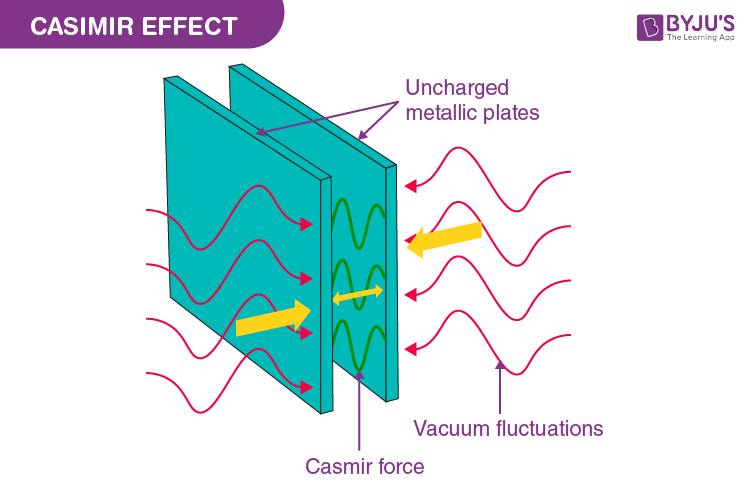
要证明零点能量存在，量子场论中最简单的实验证据是卡西米尔效应（Casimir effect）。¹

此效应是在 1948 年由荷兰物理学家 Hendrik B. G. Casimir 所提出，其考虑了一对接地、电中性金属板之间的量子化电磁场。²

在实验中，可以在两块板子间量测到一个很小的力，这种力——称之为卡西米尔力，可直接归因于板子间电磁场的零点能量变化所造成。

图片链接

（4）下图给出了势阱中粒子的波函数 \(\psi(x)\) 和粒子的概率密度 \(|\psi(x)|^2\) 的分布曲线。

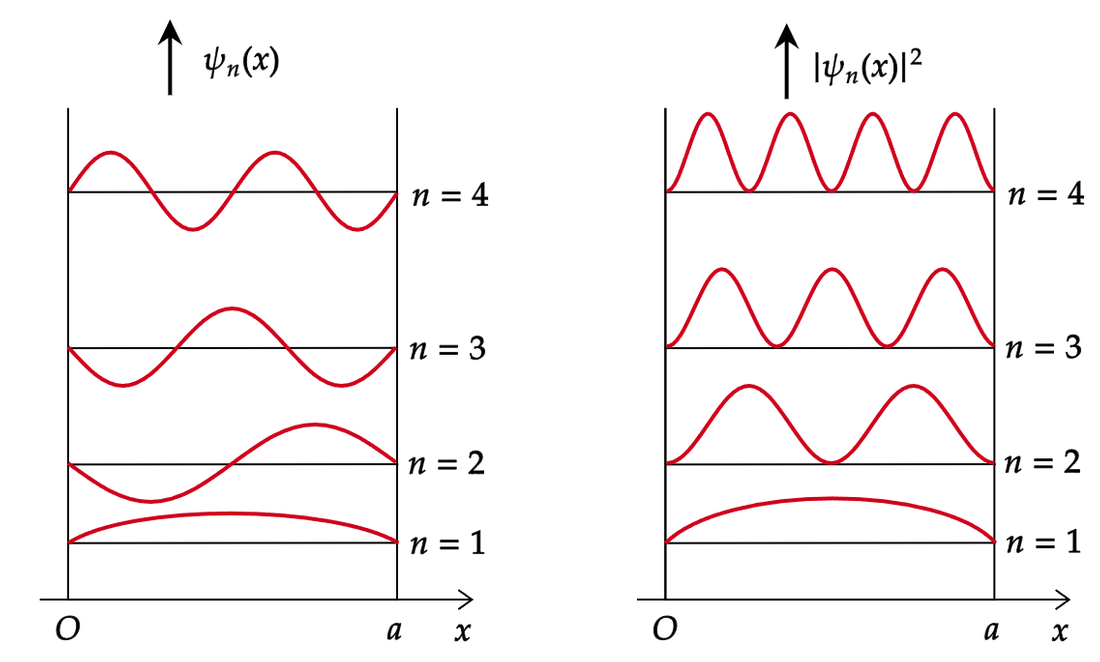
从图中可以看出，粒子出现的概率是不均匀的。

当 \(n=1\) 时，在 \(\displaystyle x=\frac{a}{2}\) 处粒子出现的概率最大；

当 \(n=2\) 时，在 \(\displaystyle x=\frac{a}{4}\) 和 \(\displaystyle x=\frac{3a}{4}\) 处概率最大；

\(\cdots\)

概率密度的峰值个数和量子数 \(n\) 相等，这又和经典概念是很不同的。

若是经典粒子，因为在势阱内不受力，粒子在两阱壁间作匀速直线运动，所以粒子出现的概率处处一样。

对于微观粒子，只有当 \(n \rightarrow \infty\) 时，粒子出现的概率才是均匀的。

而且，根据势阱中的波函数，我们还可以得到：基态波函数无节点，第一激发态有一个节点，第 \(n\) 个激发态有 \(n\) 个节点。

根据势阱中的波函数，我们还可以发现，波函数的奇偶性是交错排列的：

当 \(n=1\) 时，\(\psi(x)\) 是偶函数。

当 \(n=2\) 时，\(\psi(x)\) 是奇函数。

当 \(n=3\) 时，\(\psi(x)\) 是偶函数。

\(\cdots\)

（5）上图还表明，对无限深势阱，定态薛定谔方程的解为驻波形式，即粒子的物质波在阱中形成驻波，波函数在势阱中，只可能是半个正弦波的整数倍的状态，而且在阱壁处（\(x=0\)，\(x=a\)）对不同能量的粒子对应的波均为波节，粒子出现的概率为零。

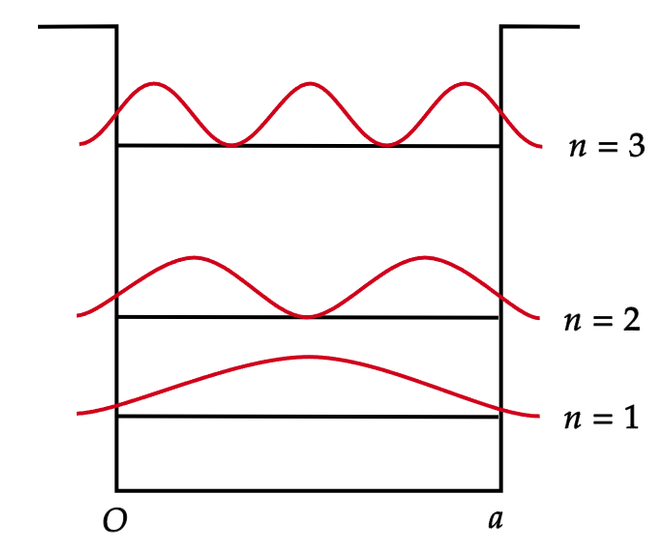
如果势阱不是无限深，粒子的能量又低于阱壁，理论证明，粒子也有到达阱外的可能，即粒子在阱外不远处出现的概率不为零。从经典理论看，这是很难理解的，但却得到了实验证实。

一维势阱是研究两维或三维势阱的基础，金属体内的自由电子可看做三维势阱中的粒子。

（6）波函数是正交归一的。

设两个轨道波函数 \(\psi_m(x)\) 和 \(\psi_n(x)\)，其中 \(m\) 和 \(n\) 是其波函数对应的轨道。

证明：

\[\begin{aligned}\displaystyle\int \psi_{m}(x)^{*} \psi_{n}(x) d x &\displaystyle =\frac{2}{a} \int_{0}^{a} \sin \left(\frac{m \pi}{a} x\right) \sin \left(\frac{n \pi}{a} x\right) d x \\&\displaystyle =\frac{1}{a} \int_{0}^{a}\left(\cos \left(\frac{m-n}{a} \pi x\right)-\cos \left(\frac{m+n}{a} \pi x\right)\right) d x \\&\displaystyle =\left.\left(\frac{1}{(m-n) \pi} \sin \left(\frac{m-n}{a} \pi x\right)-\frac{1}{(m+n) \pi} \sin \left(\frac{m+n}{a} \pi x\right)\right)\right|_{0} ^{a} \\&\displaystyle =\frac{1}{\pi}\left(\frac{\sin ((m-n) \pi)}{m-n}-\frac{\sin ((m+n) \pi)}{m+n}\right)=0\end{aligned}\]

证得：

当 \(m \neq n\) 时，\(\displaystyle\int \psi_{m}(x)^{*} \psi_{n}(x) d x=0\)。

当 \(m = n\) 时，\(\displaystyle\int \psi_{m}(x)^{*} \psi_{n}(x) d x=1\)。

上述两式子可以合并表述为：

\[\displaystyle\int \psi_{m}(x)^{*} \psi_{n}(x) d x=\delta_{m n}\]

其中 \(\delta_{m n}\)（被称作克罗内克 \(\delta\) 函数）的定义是：

\[\delta_{m n}=\left\{\begin{array}{ll}0 & \text { if } m \neq n \\1 & \text { if } m=n\end{array}\right.\]

所以，我们称波函数 \(\psi(x)\) 是正交归一的。

（7）波函数是完备的。

任何函数 \(f(x)\) 都可以写成上述波函数的线性组合。

\[\displaystyle f(x)=\sum_{n=1}^{\infty} c_{n} \psi_{n}(x)=\sqrt{\frac{2}{a}} \sum_{n=1}^{\infty} c_{n} \sin \left(\frac{n \pi}{a} x\right)\]

我们发现：\(f(x)\) 的傅里叶级数的展开也是上述形式。

如果要求上述式子的展开系数，我们可以运用波函数的正交归一性求解。

在方程两端同时乘以 \(\psi_{m}(x)^{*}\) 并积分：

\[\displaystyle \int \psi_{m}(x)^{*} f(x) d x=\sum_{n=1}^{\infty} c_{n} \int \psi_{m}(x)^{*} \psi_{n}(x) d x=\sum_{n=1}^{\infty} c_{n} \delta_{m n}=c_{n}\]

除了 \(m = n\) 项，上式使用克罗内克 \(\delta\) 函数将其他项都消去了。

所以 \(f(x)\) 得展开中的第 \(n\) 项的系数为：

\[\displaystyle c_{n}=\int \psi_{m}(x)^{*} f(x) d x\]

一维无限深势阱¶

评论