能带结构

什么是能带结构

在固体物理学中，固体的能带结构 （又称电子能带结构）描述了禁止或允许电子所带有的能量，这是周期性晶格中的量子动力学电子波衍射引起的。材料的能带结构决定了材料的多种特性。¹

图片链接

上面是二维材料 CTF/As（Covalent Triazine Frameworks/As）的能带图。

注：上图能量为 0 的位置为费米能级（\(\rm E=0~eV=E_F\)）。

能带图主要分为以下几个部分：

• 价带（Valence Band，VB）：费米能级以下的能带称为价带。
• 价带顶（Valance Band Maximum，VBM）：价带能量最高的地方称为价带顶。
• 导带（Conduction Band，CB）：费米能级以上的能带称为导带。
• 导带底（Conduction Band Minimum，CBM）：导带能量最低的地方称为导带底。
• 带隙（Band Gap）：价带顶（VBM）和导带底（CBM）之间的能量宽度称为带隙。

在非金属中，价带是电子能量的最高范围，在绝对零度时，电子通常会存在于此。而导带则是空位电子态的最低范围。在具有带隙的材料的电子能带结构图中，价带位于费米能级的下方，导带则位于其上方。

在金属中，价带和导带之间的区别并不重要，因为电导发生在一个或多个部分填充的能带中，这些能带同时具有价带和导带的性质。

图片链接

上图是在平衡状态下填充各种类型材料中的电子态。

横坐标是能量，纵坐标是态密度。

阴影遵循费米-狄拉克分布（蓝色：有状态填充，白色：无状态填充）。

窄的红色区域表示受体（p型）和供体（n型）的杂质带。

在金属和半金属中，费米能级 \(E\rm_F\) 位于至少一个带内。

在绝缘体和半导体中，费米能级位于带隙内。

在半导体中，有些能带足够接近费米能级，从而被电子或空穴填充。

如果晶体结构中有缺陷，会影响晶体的能带结构，直观的表现是在导带和价带之间出现缺陷能级。比如下面这篇文献，是在 \(\rm GaN\) 晶体中用 \(\rm C\) 或 \(\rm O\) 来替换 \(\rm N\) 原子。这样掺杂的结构就导致在带隙部分出现了缺陷能级。

图片链接

金属的能带结构

\(\rm Fe\) 的能带结构和态密度图（带隙是 \(\rm 0~eV\)）：

图片链接

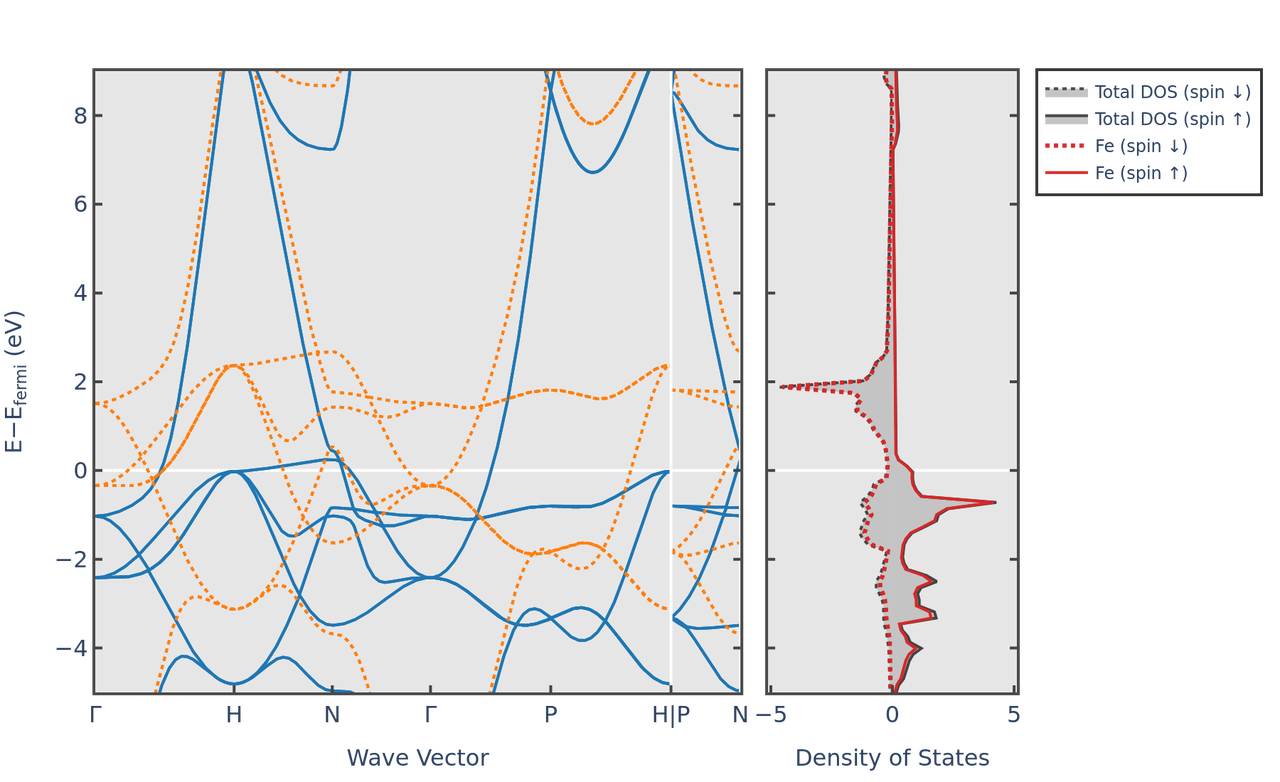
半金属的能带结构

Semimetal 和 Half-metal 目前都被翻译为半金属，但二者概念完全不同。

Semimetal 是是指导带和价带之间相隔很窄的材料，而 half-metal 则是指一些顺磁材料，它们对处于不同自旋方向的电子分别显示出金属性或非金属性。²

图片链接

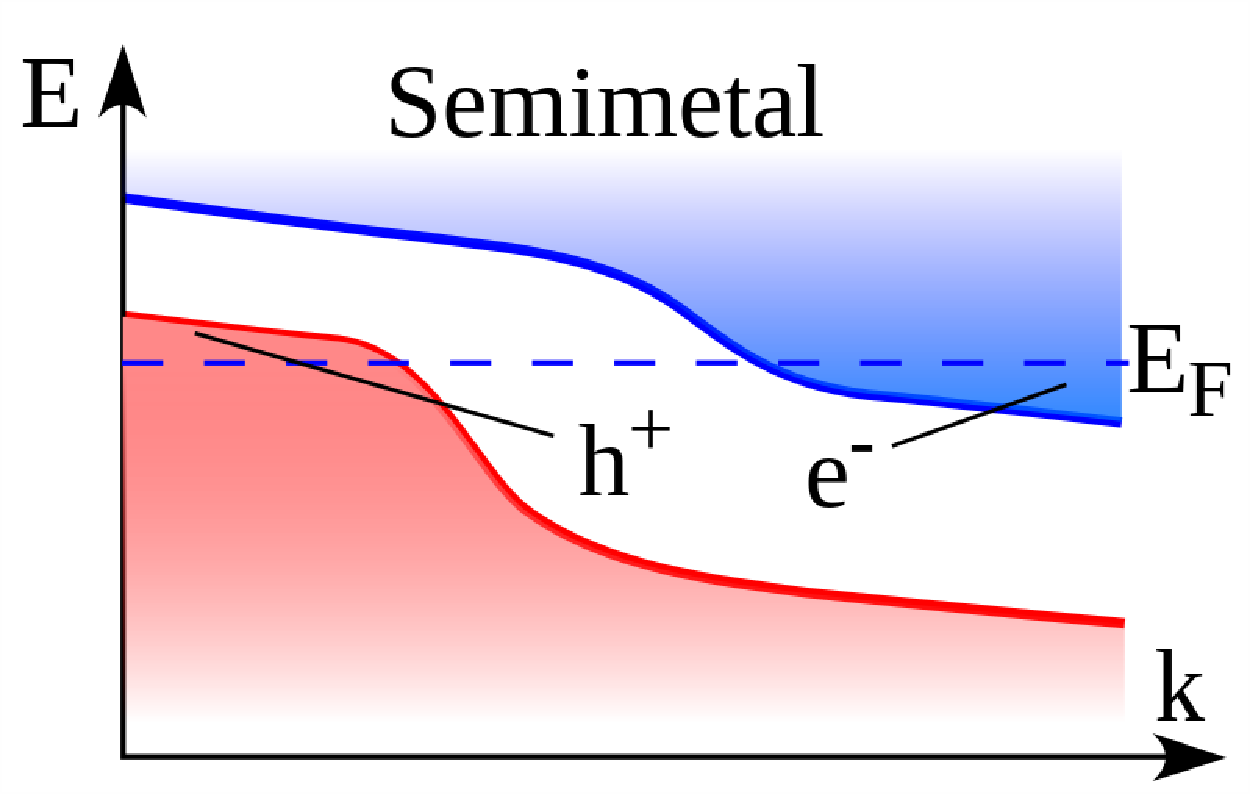
在倒空间中，Semimetal 的导带底和价带顶处于不同位置，即间接带隙。我们可以认为 Semimetal 是一种有负间接带隙的半导体，即它的导带底的能量比价带顶的低。

图片链接

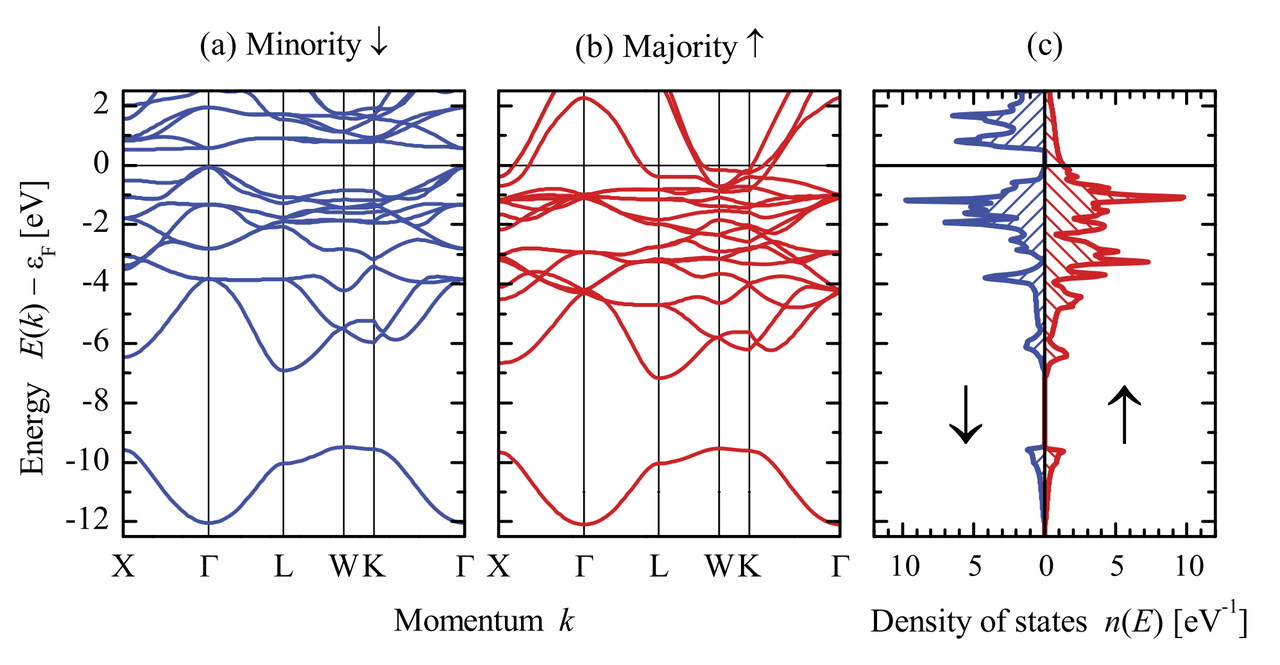
上图是半金属（Half-metal）化合物 \(\rm Co_2MnGe\) 的能带结构和态密度图。

Half-metal 是指一种材料，该材料对一种自旋方向的电子表现为导体，而对另一种自旋方向的电子表现为绝缘体或半导体。

图片链接

半导体的能带结构

\(\rm Si\) 的能带结构和态密度图（带隙是 \(\rm 0.50~eV\)）：

图片链接

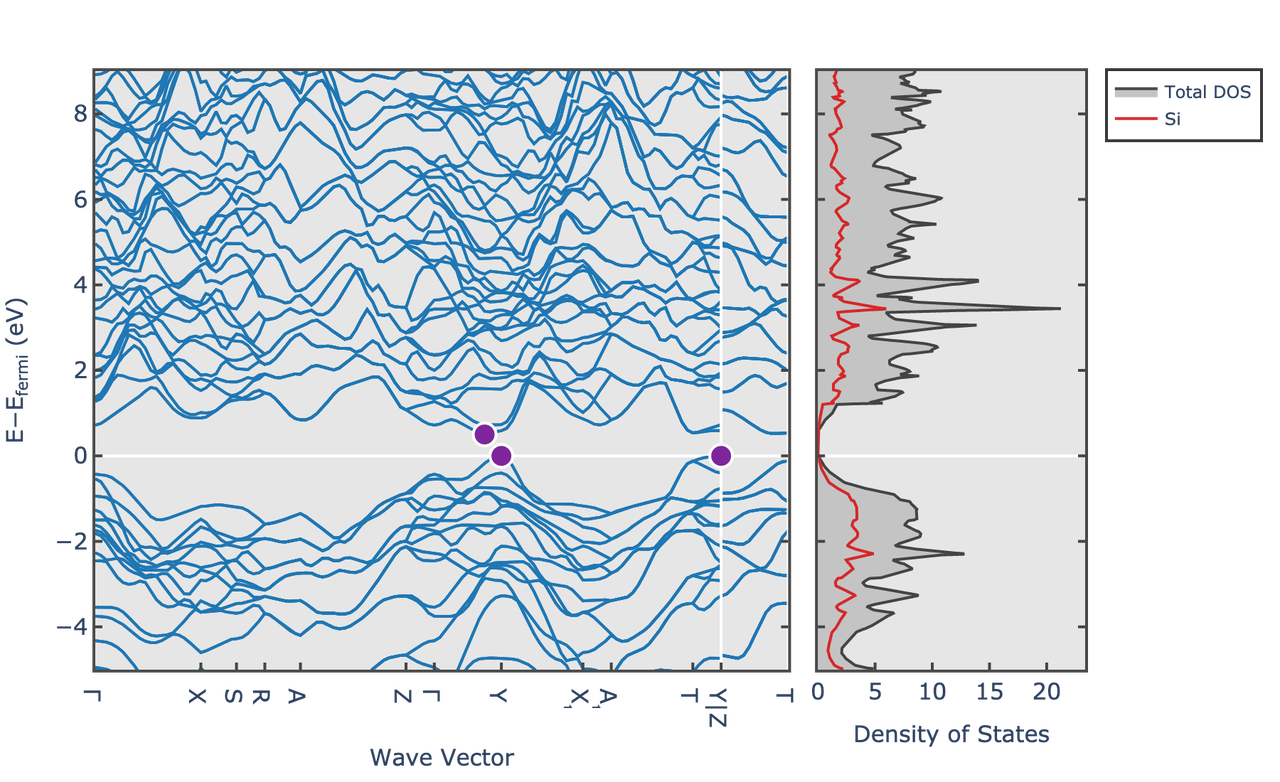
绝缘体的能带结构

\(\rm Al_2O_3\) 的能带结构和态密度图（带隙是 \(\rm 5.85~eV\)）：

图片链接

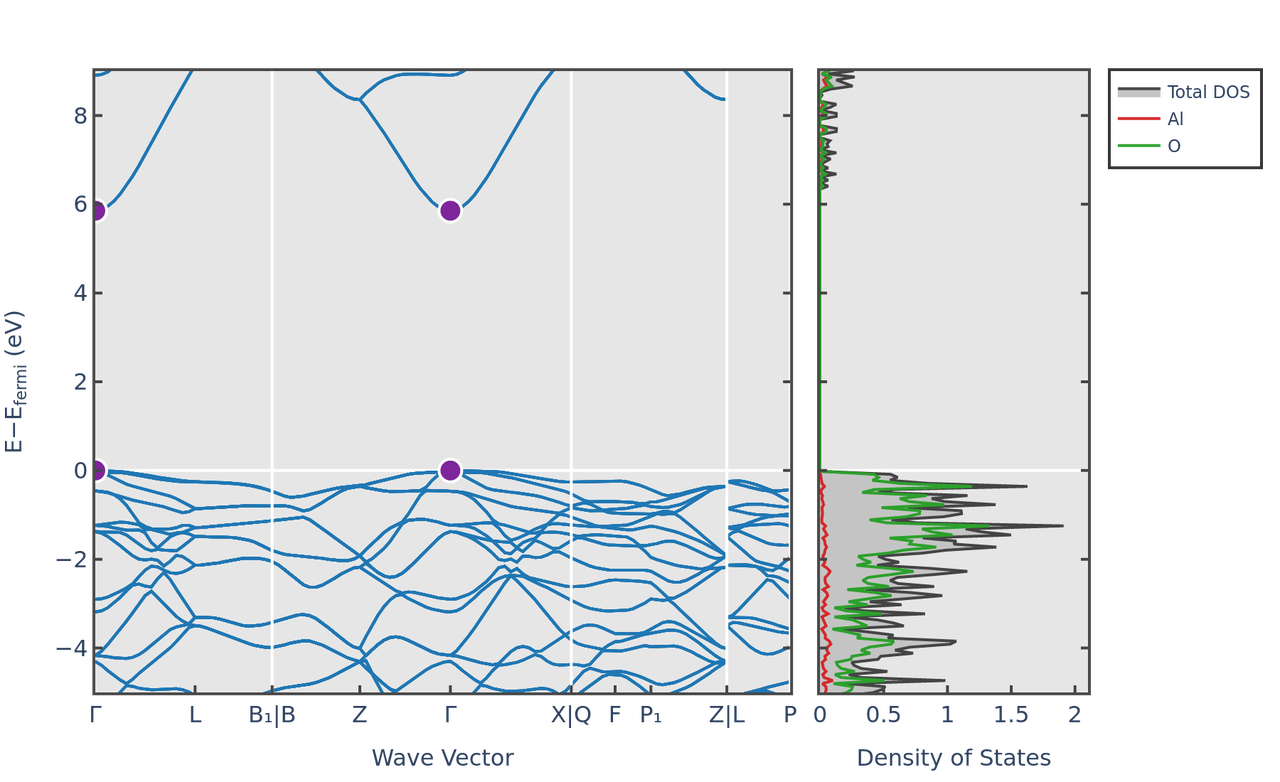
带隙

在半导体和绝缘体中，两个能带被带隙分开，而在导体中，两个能带重叠。

带隙是固体中由于能量量子化而不能存在电子态的能量范围。

在能带的概念中，价带和导带之间的能隙就是带隙。

非金属的电导率由电子从价带激发到导带的敏感性决定。

直接带隙和间接带隙

判断方法：价带顶和导带底是否位于同一个波矢 \(\rm k\)。位于同一个波矢则为直接带隙，不同波矢为间接带隙。

图片链接

区别：

• 直接带隙在进行电子跃迁的时候不需要释放或吸收声子；
• 间接带隙在进行电子跃迁的时候需要释放或吸收声子；

为什么间接带隙电子的跃迁需要声子的参与？

电子的跃迁过程需要遵循两个守恒：

能量守恒：\(E_{final}-E_{initial}=E_{photon}\)

动量守恒：\(\hbar \vec{k}_{final}-\hbar \vec{k}_{initial}=\hbar \vec{k}_{\text {photon }}\)

电子或空穴在布里渊区的波矢 \(k\) 的量级为：\(\displaystyle k \sim \frac{2\pi}{a} \sim 10^{10} \mathrm{~cm}^{-1}\)

可见光的波矢 \(k\) 的量级为：\(\displaystyle k \sim \frac{2\pi}{\lambda} \sim 10^{7} \mathrm{~cm}^{-1}\)

所以动量守恒可以化简为：\(\hbar \vec{k}_{final}-\hbar \vec{k}_{initial}=0\)

上式说明，电子跃迁前后的动量近似相等的。

但是间接带隙在跃迁的时候，波矢 \(k\) 是变化的。

所以必然有除了光子和电子的第三方来为电子提供动量来维持动量守恒。

因为描述晶格振动的声子的动量与电子的动量是同量级的，所以这个第三方是声子。

所以间接带隙在进行电子跃迁的时候需要释放或吸收声子来维持动量守恒。³

视野拓展

另外我们可以通过各种手段使材料的能带结构在直接带隙和间接带隙之间相互转换。

比如单层 \(\rm MoS_2\) 材料，我们可以对改材料施加机械应力来调节改材料的能带结构。⁴

图片链接

从上图我们可以发现，在 0 应力下，单层 \(\rm MoS_2\) 是直接带隙能带结构，在 \(2\%\) 的应力下，单层 \(\rm MoS_2\) 是间接带隙能带结构。

有效质量

经典力学

电子受到电场的作用，根据牛顿定律，我们可以写出：

\[\displaystyle F=-e \cdot E=m \cdot \frac{d^{2} \vec{r}}{d t^{2}}\]

\(\vec{r}\) 是电子的位置矢量。

我们也可以得出动量有关的形式：

\[ \begin{array}{ll}\displaystyle\vec{p}=m\frac{d \vec{r}}{d t}\\\displaystyle\vec{F}=-e\cdot E=\frac{d \vec{p}}{d t}\end{array} \]

群速度

该章节参考的文章链接：https://en.wikipedia.org/wiki/Group_velocity

在量子力学中，粒子的速度可以被认为是粒子波包的群速度 \(\rm\mathbf{v}_{group}\)。

在一维情况，群速度由以下方程定义：

\[\displaystyle v_{\mathrm{group}} \equiv \frac{\partial \omega}{\partial k}\]

其中 \(\omega\) 是波的角频率，\(k\) 是角波数。

在三维情况，群速度由以下方程定义：

\[\mathbf{v}_{\mathrm{group}}=\nabla_{\mathbf{k}} \omega\]

\(\nabla_{\mathbf{k}} \omega\) 是角频率的梯度，\(\bf k\) 是波矢。

波的群速度是波振幅的整体包络形状（称为波的调制或包络）在空间中传播的速度。

图片链接

绿色小球以群速度 \(\rm\mathbf{v}_{group}\) 传播。

红色方块以相速度移动。

图片链接

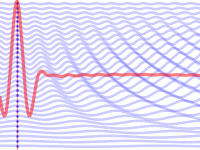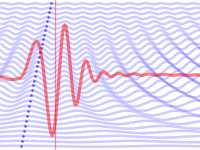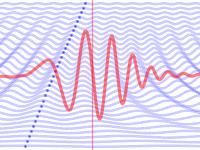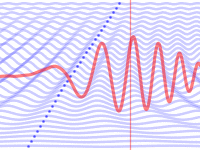
红线以群速度 \(\rm\mathbf{v}_{group}\) 传播。

蓝点以相速度移动。

理论推导

该章节参考的文章链接：https://en.wikipedia.org/wiki/Effective_mass_(solid-state_physics)

在晶体中，晶体动量的定义为：\(\mathbf{p}_{\text {crystal }} \equiv \hbar \mathbf{k}\)

晶体动量随时间的变化率：

\[\displaystyle\mathbf{F}=\frac{\mathrm{d} \mathbf{p}_{\text {crystal }}}{\mathrm{d} t}=\hbar \frac{\mathrm{d} \mathbf{k}}{\mathrm{d} t}\]

群速度 \(\rm\mathbf{v}_{group}\) 随时间的变化率：

\[\displaystyle\mathbf{a}=\frac{\mathrm{d}}{\mathrm{d} t} \mathbf{v}_{\mathrm{group}}=\frac{\mathrm{d}}{\mathrm{d} t}\left(\nabla_{k} \omega(\mathbf{k})\right)=\nabla_{k} \frac{\mathrm{d} \omega(\mathbf{k})}{\mathrm{d} t}=\nabla_{k}\left(\frac{\mathrm{d} \mathbf{k}}{\mathrm{d} t} \cdot \nabla_{k} \omega(\mathbf{k})\right)\]

根据公式 \(E(\mathbf{k})=\hbar \omega(\mathbf{k})\)，我们可以得到：\(\displaystyle \frac{E(\mathbf{k})}{\hbar}= \omega(\mathbf{k})\)

将 \(\displaystyle\mathbf{F}=\frac{\mathrm{d} \mathbf{p}_{\text {crystal }}}{\mathrm{d} t}=\hbar \frac{\mathrm{d} \mathbf{k}}{\mathrm{d} t}\) 和 \(\displaystyle \frac{E(\mathbf{k})}{\hbar}= \omega(\mathbf{k})\) 带入 \(\displaystyle\mathbf{a}=\nabla_{k}\left(\frac{\mathrm{d} \mathbf{k}}{\mathrm{d} t} \cdot \nabla_{k} \omega(\mathbf{k})\right)\) 上式，我们可以得到：

\[\mathbf{a}=\nabla_{k}\left(\frac{\mathbf{F}}{\hbar} \cdot \nabla_{k} \frac{E(\mathbf{k})}{\hbar}\right)=\frac{1}{\hbar^{2}}\left(\nabla_{k}\left(\nabla_{k} E(\mathbf{k})\right)\right) \cdot \mathbf{F}=M_{\text {inert }}^{-1} \cdot \mathbf{F}\]

从上式，我们可以得到质量的张量形式：

\[\displaystyle M_{\text {inert }}^{-1}=\frac{1}{\hbar^{2}} \nabla_{k}\left(\nabla_{k} E(\mathbf{k})\right)\]

张量中的每个元素可以表示为：

\[\displaystyle\left[M_{\text {inert }}^{-1}\right]_{i j}=\frac{1}{\hbar^{2}}\left[\nabla_{k}\left(\nabla_{k} E(\mathbf{k})\right)\right]_{i j}=\frac{1}{\hbar^{2}} \frac{\partial^{2} E}{\partial k_{i} \partial k_{j}}\]

这个张量允许加速度和力在不同的方向上，并且加速度的大小取决于力的方向。

对于抛物型各向同性带：

\[\displaystyle M_{\text {inert }}{ }^{-1}=\frac{1}{m^{*}} \mathbf{I}\]

其中 \(m^*\) 是标量有效质量，\(\bf I\) 是单位张量。

有效质量是通过色散关系的曲率来定义的。具体来说，它是电子能量对波矢的二次导数的倒数。在抛物线近似下，这个二次导数是常数，这使得计算有效质量变得直接和简单。而对于非抛物线能带，曲率会随着波矢的变化而变化，计算起来更复杂。

在能带的极点附近（通常是导带底部或价带顶部），这种关系可以近似为抛物线形式。这是因为在这些极点附近，能量与动量的二次项占主导，而更高阶的项可以忽略。

图片链接

通过上图，我们可以发现，这种抛物线求解有效质量的方法不仅可以求解电子的有效质量，还可以求解空穴的有效质量。

物理意义：在抛物线近似下，有效质量提供了一个清晰的物理图像，即电子在晶体中的行为就像在真空中的自由电子，但具有不同的（有效的）质量。这大大简化了电子动力学的描述，并有助于理解和预测电子在材料中的行为。

狄拉克锥

石墨烯中 $\pi$ 键的能量色散关系

图片链接

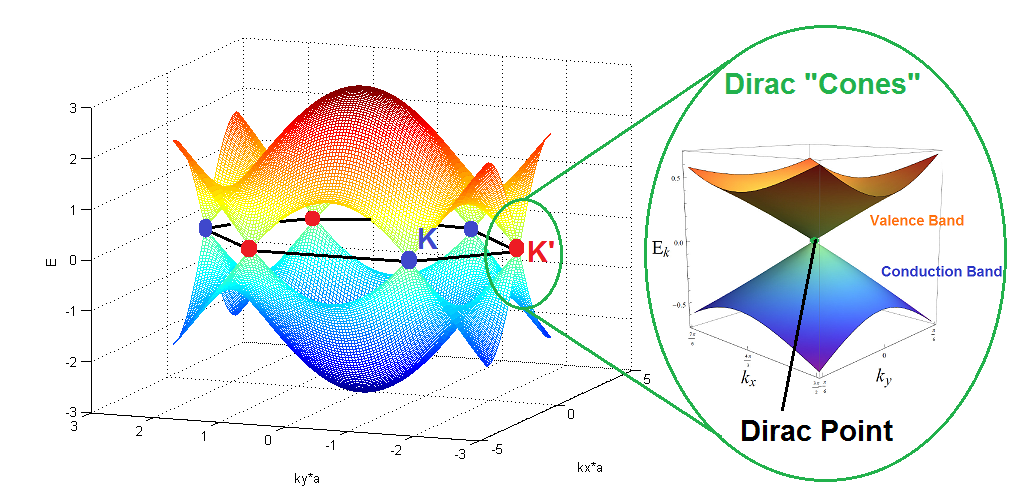
在能带结构中，狄拉克锥描述价带和导带的能量在二维晶格 \(k\) 空间中，除了狄拉克点所在的位置外，其他任何动量的价带和导带能量都不相等。由于在能带结构中呈现上下对顶的圆锥形，并且这种能带结构满足描述相对论粒子能量-动量关系的狄拉克方程，因此被称为狄拉克锥。

（a）石墨烯的晶体结构；（b）石墨烯的能带结构；

图片链接

图片链接

狄拉克锥最早是在 Andre Geim 和 Konstantin Novoselov 制备出来的石墨烯中发现的。

在 2010 年，Andre Geim 和 Konstantin Novoselov 凭借“关于二维材料石墨烯的开创性实验”获得诺贝尔物理学奖。

左：Andre Geim；右：Konstantin Novoselov；

图片链接

理论

该章节参考的文章链接：http://www.360doc.com/content/18/0420/11/11935121_747247286.shtml

根据狭义相对论，电子的能量可以表示为：

\[E^{2}=c^{2} p^{2}+m_{0}^{2} c^{4}\]

其中 \(m_0\) 是静止质量。

根据上式，我们可以得出电子的能量为：

\[E= \pm \sqrt{c^{2} p^{2}+m_{0}^{2} c^{4}}\]

这里出现了负能量解，狄拉克认为负能量的解是存在的，只不过都被电子占据了。这种情况对应的是 “真空” ，即看起来没有电子。如果处于负能量的电子被激发出来，吸收光的能量后跃迁到能量大于零的状态，对应的就是 “电子-空穴”对的产生，因为这时负能量的状态看起来少了个电子，等效的就是一个带正电的空穴，或者叫反电子。

这样的物理图景本来是狄拉克用来解释自己的关于电子的理论的，但后来人们发现在固体物理求解的时候，固体中电子的能级会密密麻麻地形成能级，看起来就是一个一个的能带，假设有两个能带，上面的叫导带，下面的叫价带，价带的电子可以看做是能量小于零的，而导带的电子可以看做是能量大于零的，费米能级 \(E\rm_F\) 则被定义为能量的零点。

在这样的一幅图像下，如果价带顶的一个电子被激发到导带底，看起来就好像是在价带产生了一个空穴，而在导带产生了一个电子，这个图像和狄拉克关于电子的相对性理论正好可以对应上。

我们可以定义带隙为:

\[\Delta=m_{0} c^{2}\]

电子的能量可以表示为：

\[E(k)= \pm \sqrt{c^{2} \hbar^{2} k^{2}+\Delta^{2}}\]

上式中正号对应的是导带电子的色散关系，负号对应的是价带电子的色散关系。根据能带理论，电子的色散关系是被量子力学计算修正了的，这意味着电子的质量会发生改变，或我们需要用电子的有效质量来代替电子的“裸质量”。

假设 \(k\) 很小，我们对狄拉克电子正能量的解展开:

\[\begin{array}{ll}E(k)&\displaystyle =\Delta \sqrt{1+\left(\frac{c \hbar k}{\Delta}\right)^{2}} \\&\displaystyle \approx \Delta\left(1+\frac{1}{2}\left(\frac{c \hbar k}{\Delta}\right)^{2}\right)\\&\displaystyle =\Delta+\frac{c^{2} \hbar^{2} k^{2}}{2 \Delta}\\\end{array}\]

假设光速为 1 ,即 \(c=1\) 我们得到：

\[\displaystyle E(k)=\Delta+\frac{\hbar^{2} k^{2}}{2 \Delta}=m_{0}+\frac{\hbar^{2} k^{2}}{2 m_{0}}\]

换句话说只要能隙不为 0 ，电子（或更严格地应该叫准电子）在导带底处的色散关系就是“自由粒子”。

根据能带计算，导带底和价带顶也可能接上，并形成两个雉形 “头对头” 的形状，此时带隙为 0 （或电子的有效质量为 0 ）：

\[ \begin{array}{ll}\Delta=m_{0} c^{2}=0\\E(k)= \pm c p= \pm c \hbar k= \pm \alpha k\end{array} \]

即色散关系与波矢 \(k\) 成正比。

当电子有效质量为 0 的时候，准电子的迁移率会很大。这是因为电子迁移率 \(\mu\) 被定义为单位电场获得的漂移速度：

\[\displaystyle\mu=\frac{v_{d}}{E}=\frac{\tau e}{m^{*}}\]

根据上式，我们可以发现，当有效质量 \(m^*=0\) 的时候，电子迁移率 \(\mu\) 趋向于无穷大。

---

1. https://zh.wikipedia.org/wiki/%E8%83%BD%E5%B8%A6%E7%BB%93%E6%9E%84 ↩

2. https://zh.wikipedia.org/wiki/%E5%8D%8A%E9%87%91%E5%B1%9E_(%E8%83%BD%E5%B8%A6%E7%90%86%E8%AE%BA) ↩

3. https://www.coursera.org/lecture/semiconductor-physics/radiative-transitions-KszjA ↩

4. https://www.nature.com/articles/s41699-019-0123-5 ↩

评论