什么是声子?¶
声子(Phonon)是晶体中晶体结构集体激发的准粒子,化学势为零,服从玻色-爱因斯坦统计,是一种玻色子。声子本身并不具有物理动量,但是携带有准动量 \(\hbar \mathbf{q}\),并具有能量 \(\hbar\omega\)(其中 \(\hbar\) 为约化普朗克常数)。
根据 Nambu-Goldstone Theorem,任何连续性整体对称性的自发破缺,必然对应一个零质量的玻色子。声子就是平移对称性被晶格的点阵结构自发破缺以后对应的玻色子。1

在考虑晶体中原子振动之前,我们采用的是静止晶格模型。
因为原子核的质量比电子的质量大得多,所以静止晶格模型采用的是绝热近似。
绝热近似:考虑电子运动时可不考虑原子核的运动。原子核固定在它的瞬间位置。
电子相关的性质,静止晶格模型一般都可以较好的描述。
但是静止晶格模型也有局限性。
从经典理论出发,我们发现只有在绝对零度的时候,原子才是静止的。
从量子力学出发,我们发现即使在绝对零度,根据测不准原理,原子也不是静止的,具有零点振动。
所以静止晶格模型只是一种比较粗略的近似。
从量子理论出发,为了更好的描述晶体的物理性质,我们需要考虑晶体中原子的振动。
但是晶体的中原子的振动也是很复杂的,在描述原子振动的同时,我们也需要引入一种近似,即简谐近似——力与位移呈线性关系。
基于简谐近似,我们观察到晶体内的原子展现出 N 种集体振动模式,这些模式以波矢为变量 \(\rm\omega(q)\)。在同一种模式下,不同原子仅在相位上存在差异。
在引入简谐近似后,我们发现原子在任何时刻都不再是完全的周期性排列,每个原子都在做简谐振动。
在量子力学的基础上,我们对原子的简谐振动进行量子化。之后,我们可以发现简谐振动的能量是分裂的。我们称这每一个分裂的能量是简谐振动能量子,即声子。
每个声子都对应于晶体格点的一种集体振动模式,对应着特定的能量和动量。在这种情况下,声子可以被视为晶格振动的激发状态,每个声子代表了该特定振动模式的一个量子化能级。这样,声子就成为了描述和分析晶体中这种特定振动模式能量和动量传递的有用工具。
一维单原子链¶
设 \(n\) 为整数,共有 N 个原胞。
简谐势: \(\displaystyle V^{\text {简谐}}=\sum_{n} \frac{1}{2} \beta\left(x_{n}-x_{n+1}\right)^{2}\)
运动方程: \(\displaystyle m \frac{d^{2} x_{n}}{d t^{2}}=\beta\left(x_{n+1}+x_{n-1}-2 x_{n}\right)\)
尝试解: \(\displaystyle x_{n}(t)=A e^{i[qna-\omega(q) t]}\)
振动模式: \(\displaystyle \omega(q)=2 \sqrt{\frac{\beta}{m}} \Bigg|\sin \frac{q a}{2}\Bigg|\)
其中 \(\displaystyle q=\frac{l}{N} \frac{2 \pi}{a}\)\(,\)\(\displaystyle-\frac{N}{2}<l \leq \frac{N}{2}\),并且 \(l\) 取整数。
不等价的 \(q\) 一共有 N 个。
根据解的形式 $ x_{n}(t)=A e^{i[qna-\omega(q) t]}$,我们可以得到结论:
- 各个原子的振动并不独立,与第 \(n\) 个原胞有关。
- 如果格矢 \(na\) 相差为 \(\displaystyle \frac{2\pi}{q}\) 的整数倍的时候,位移完全相等。
实际上解 \(x_{n}(t)=A e^{i[q na-\omega(q)t]}\) 只是一个特解,一般解应是它的叠加。
在任意时刻 \(t\),\(n\) 格点的原子的一般解为:\(\displaystyle x_{n}(t)=\sum_{q} A_{q}(t) e^{i q n a}\)
根据一般解的形式,我们发现:
- 振幅与 \(q\) 有关,\(A_q(t)\) 中含有 \(e^{-i\omega t}\)。
- 位移是各种不同波矢、不同频率的格波的叠加。
根据振动模式 \(\displaystyle\omega(q)=2 \sqrt{\frac{\beta}{m}} \Bigg|\sin \frac{q a}{2}\Bigg|\),我们可以发现振动频率 \(\omega(q)\) 与原胞(原子)完全无关。不同的振动频率是根据不同的波矢 \(q\) 来进行区分的。
通过对一维单原子链的分析,我们可以发现:在同种波矢 \(q\) 下,所有的原子都同时在做频率为 \(\omega(q)\) 的振动,只不过不同原子间存在相位差。晶格振动是一种集体振动!
通过简正坐标,我们可以把所有关联的原子位移用一个整体的位移来描写,即把所有原子的位移以某种形式组合起来,用这种整体位移来描写这个本质上是独立的振动。具体是通过与每个原胞有关的变量为坐标轴的 N 维坐标系来建立简正坐标。
用本征矢 \(e^{iqna}\) 做基轴:\(\displaystyle\frac{1}{\sqrt{N}} e^{\text {iqna }}\)
本征矢 \(e^{iqna}\) 本身满足正交归一性:
- 按 \(q\) 求和: \(\displaystyle \frac{1}{N} \sum_{q} e^{i q\left(n-n^{\prime}\right) a}=\delta_{n, n^{\prime}}\)
- 按 \(n\) 求和: \(\displaystyle\frac{1}{N} \sum_{n} e^{i\left(q-q^{\prime}\right) \mathrm{ma}}=\delta_{q, q^{\prime}}\)
我们可以写出简正坐标形式的位移:
\(Q_{q}(t)\) 就是简正坐标。
利用正交条件,我们可以求出 \(Q_{q}(t)\) 的具体形式:
将 \(\displaystyle x_{n}(t)=\frac{1}{\sqrt{N m}} \sum_{q} Q_{q}(t) e^{i q na}\) 带入 \(\displaystyle T=\frac{1}{2} \sum_{n} m \dot{x}_{n}^{2}\),我们可以得到在简正坐标下的动能:
将 \(\displaystyle x_{n}(t)=\frac{1}{\sqrt{N m}} \sum_{q} Q_{q}(t) e^{i q na}\) 带入 \(\displaystyle\rm V=\frac{\beta}{2} \sum_{n}\left(x_{n+1}^{2}+x_{n}^{2}-2 x_{n+1} x_{n}\right)\),我们可以得到在简正坐标下的势能:
其中 \(\displaystyle \omega_{q}^{2}=\frac{2 \beta}{m}[1-\cos (q a)]\)。
利用共轭关系 \(Q_{-q}=Q_{q}^{*}\),我们可以得到简正坐标下的哈密顿量:
\(\displaystyle H=\frac{1}{2} \sum_{q}\left(\left|\dot{Q}_{q}\right|^{2}+\omega_{q}^{2}\left|Q_{q}\right|^{2}\right)\)
其中 \(\displaystyle \omega_{q}^{2}=\frac{2 \beta}{m}[1-\cos (q a)]\)。
我们发现上述哈密顿量类似于量子力学的谐振子所对应的哈密顿量。
过渡到量子力学处理——简谐振子方程
解得能量:\(\displaystyle E\left(\omega_{q}\right)=\left(n_{q}+\frac{1}{2}\right) \hbar \omega_{q}\)
注:量子化谐振子的频率就是经典简谐振动的频率。
三维¶
定义简正坐标 \(Q_n\);
\(j\) 是表示某一个方向。
通过线性变换消除交叉项,将动能和势能同时简化为简正坐标 \(Q_n\) 平方项的和。
动能:\(\displaystyle T=\frac{1}{2} \sum_{n=1}^{3 N} \dot{Q}_{n}^{2}\)
势能:\(\displaystyle V=\frac{1}{2} \sum_{n=1}^{3 N} \omega_{n}^{2} Q_{n}^{2}\)
正则动量: \(\displaystyle p_{n}=\frac{\partial(T-V)}{\partial \dot{Q}_{n}}=\dot{Q}_{n}\)
哈密顿量: \(\displaystyle H=\frac{1}{2} \sum_{n=1}^{3 N}\left(p_{n}^{2}+\omega_{n}^{2} Q_{n}^{2}\right)\)
通过正则动量得到:
晶格振动的量子化¶
将经典哈密顿中的动量写成算符的形式: \(\displaystyle p_{n}=-i \hbar \frac{\partial}{\partial Q_{n}}\)
之后,我们就可以得到波动方程:
这表示的是一系列无相互作用的简谐振子,可以分离变量,记:
我们可以得到:
解为厄米多项式,其本征值为:\(\displaystyle \varepsilon_{l}=\left(n_{l}+\frac{1}{2}\right) \hbar \omega_{l}\)(第 \(l\) 支格波的能量)
格波的能量是分立的,以 \(\hbar\omega_l\) 为整数倍的增加。
根据上式,我们可以发现:振动能量是分立的,量子化的!
其中,\(\omega_{l}\) 是声子的振动频率,\(\hbar \omega_{l}\) 是声子的能量。
声子是玻色子¶
声子和声子之间没有相互作用(相互独立的)。
就相互作用这方面说,声子与自由电子非常接近,但是声子与自由电子的统计方式完全不一样。
声子是描写晶体中所有原子集体振动的量子。
声子包含原子周期性排列结构的信息。
考虑振动能量:以频率 \(\rm \omega\) 振动,能量是量子化的:
半经典处理:声子能量分立,但用经典统计。根据玻尔兹曼统计理论,略去常数项以后,在温度为 \(T\) 时,一个频率 \(\omega\) 的振动模式的平均能量为:
上式中 \(\displaystyle \beta=\frac{1}{k_{\mathrm{B}} T}\)。
常用的关系: \(\displaystyle \frac{\sum n e^{-n \beta}}{\sum e^{-n \beta}}=-\frac{\partial}{\partial \beta} \ln \sum e^{-n \beta}=-\frac{\partial}{\partial \beta} \ln \frac{1}{1-e^{-\beta}}=\frac{1}{e^{\beta}-1}\)
根据上式,我们可以得到: \(\displaystyle\bar{E}(\omega)=\frac{\displaystyle\sum_{n=0}^{\infty}\rm n \hbar \omega e^{-n h \omega \beta}}{\displaystyle\sum_{n=0}^{\infty} \rm e^{-n h \omega \beta}}=\frac{\hbar \omega}{e^{ \hbar \omega\beta}-1}\)
对于 N 个原子,每个原子有 3 个自由度,共有 3N 个振动模式:
如比较 \(\displaystyle U=\sum_{i=1}^{3 N} n \hbar \omega_{i}\),我们得到 \(\displaystyle n=\frac{1}{e^{\hbar \omega_i \beta}-1}\) 正是声子能量之和,如果 \(n\) 是声子占据数。
\(n\) 是声子占据数,\(U\) 是声子能量之和。
晶体的热学性质与晶格振动有关的部分由此给出。
最低能量并不是零,而是 \(\displaystyle\frac{\hbar\omega_l}{2}\)。我们称其为零点振动能。
声子谱¶
声子谱是指在固体材料中,声子的能量与其动量(或波矢)之间的关系。它展示了声子的能量(通常表示为频率)随其波矢变化的方式。声子谱是研究晶体动力学和热力学性质的重要工具,因为它直接关联了晶体中的振动模式与物质的各种物理特性。
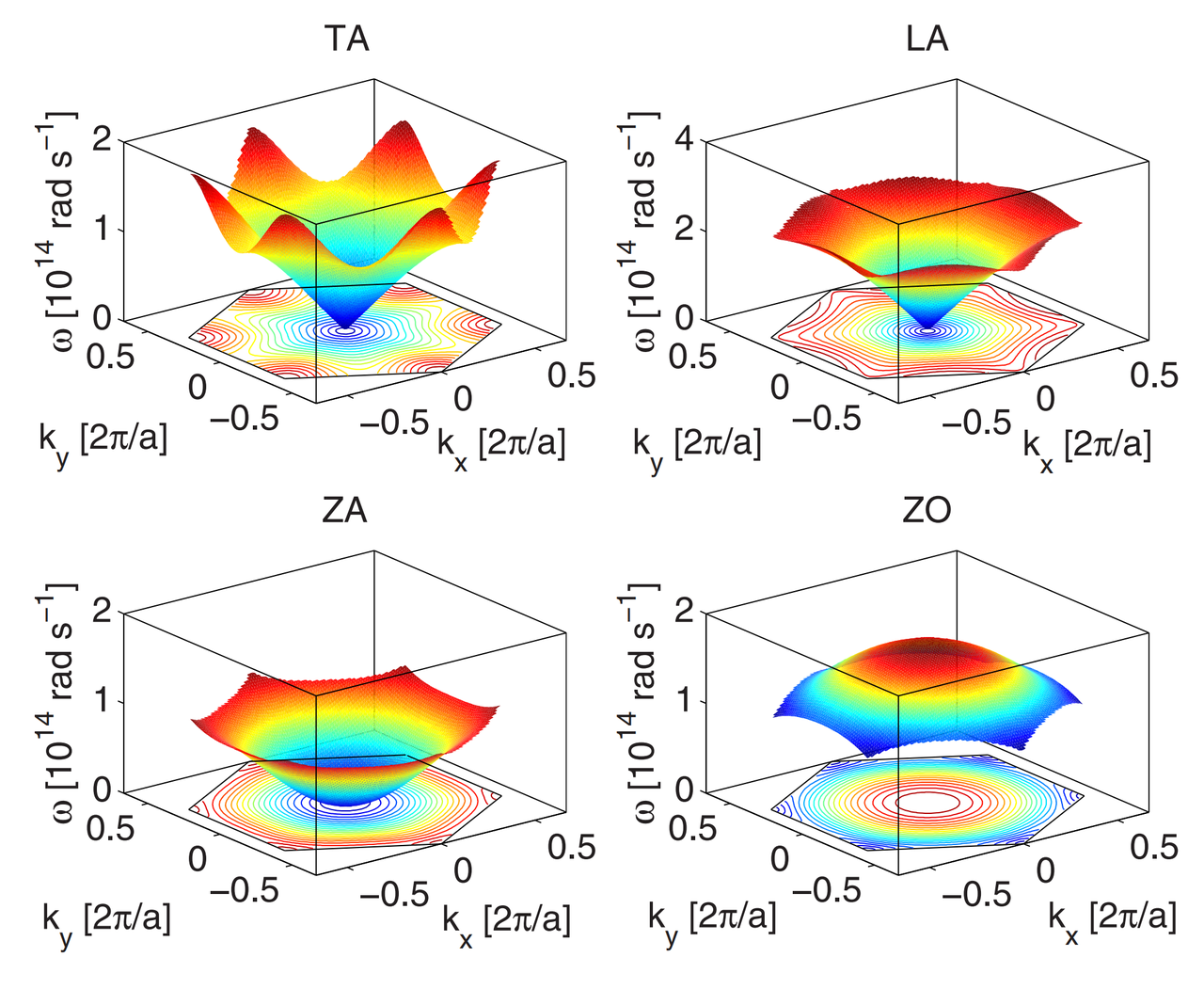
上图展示了石墨烯第一布里渊区上的 TA、LA、ZA 和 ZO 分支。色散是强各向异性的,导致声子群速度(由径向频率的梯度给出)强烈依赖于声子波矢量的方向。剩余的两个光学分支(TO 和 LO)由于其对热输运的贡献可以忽略不计,因此未画出。
下图的实线部分是石墨烯的二维声子谱:
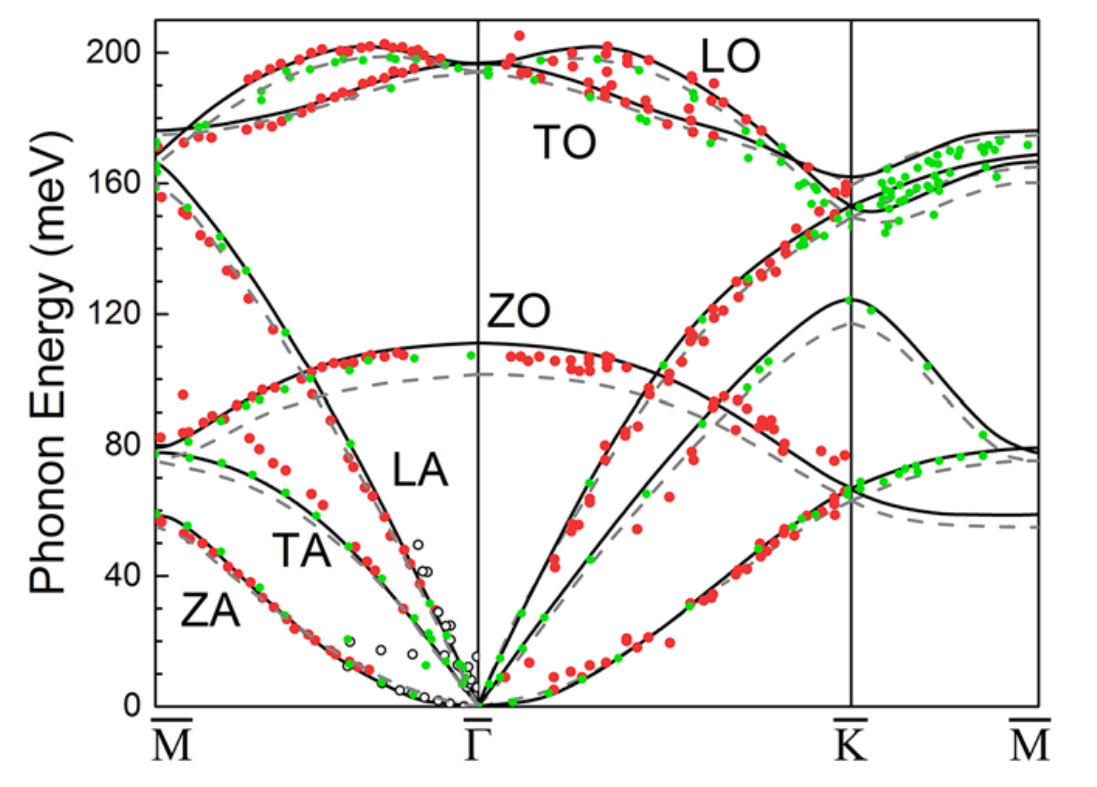
声子谱不仅可以在计算上得到,也可以在实验上通过测量得到。
石墨烯的二维声子谱中的数据点就是通过实验测得:
- 红点:高分辨率电子能量损失谱(HREELS);
- 绿点:非弹性x射线散射;
- 白点:非弹性中子散射;
声子谱中每一个数据点就代表一种振动态:

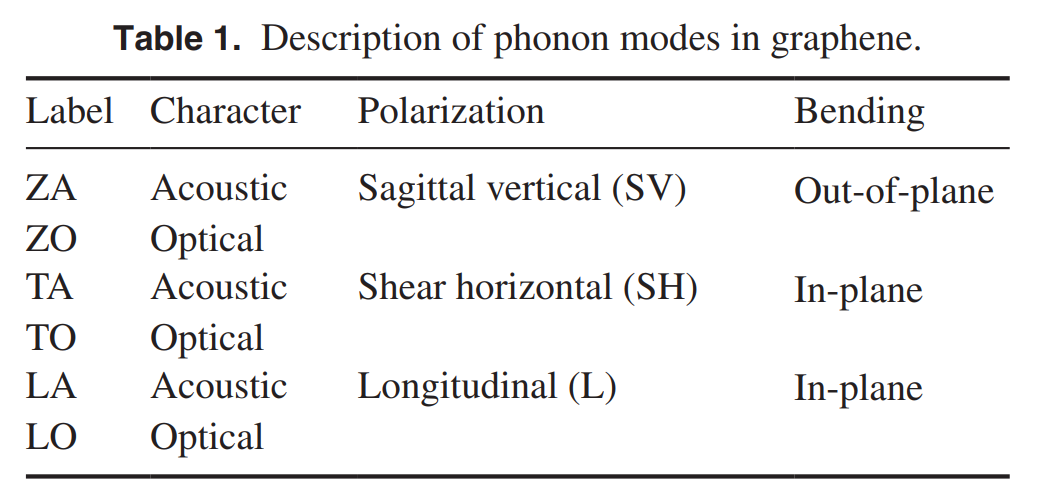
我们可以看到 ZA、TA 和 LA 是声学模式,ZO、TO 和 LO 是光学模式。
在声子谱中,声学模式和光学模式的区别在哪里?
在声子谱中,声学模式和光学模式的主要区别在于它们的原子振动模式和频率范围。
声学模式:
- 原子振动:在声学模式中,晶格中的原子以相同的方向和相近的相位振动。这意味着相邻的原子会同步移动,类似于声波在材料中传播的方式。
- 频率范围:声学模式通常出现在声子谱的低频部分。随着波矢量(晶格波的动量)接近零,它们的频率也趋于零。
光学模式:
- 原子振动:在光学模式中,晶格中不同类型的原子以相反方向振动,这导致电偶极矩的变化。这种振动模式对于具有多种原子类型的复杂晶格很重要。
- 频率范围:光学模式出现在声子谱的高频部分。即使当波矢量接近零,它们的频率也不为零,通常比声学模式的频率高。
通过上面的石墨烯的二维声子谱图,我们可以发现声学模式的确在低频部分。即使当波矢量接近零,光学模式的频率也不为零,即光学模式出现在声子谱的高频部分。
缺陷和畸变对声子谱有何影响?
缺陷和畸变在晶体中的存在对声子谱有显著影响,因为它们改变了晶体的周期性和对称性,从而影响声子的行为。
缺陷对声子谱的影响:
- 局部模式:晶体中的缺陷(如空位、杂质或替换原子)可以引入所谓的局部模式。这些模式是声子谱中原本不存在的频率,它们与缺陷相关的局部振动有关。
- 散射中心:缺陷可以作为声子散射的中心。这种散射影响声子的平均自由程,进而影响材料的热导率和其他热力学性质。
- 能带扁平化:在缺陷附近,声子的色散关系可能会出现扁平化,这意味着在某些频率范围内,声子的能量几乎不随波矢改变。
畸变对声子谱的影响:
- 对称性破坏:晶体结构的畸变(如晶格扭曲或应力)可以破坏晶体的对称性,这可能导致一些原本被禁止的声子模式变得允许,或者改变现有模式的频率。
- 能隙的形成或变化:在声子色散关系中,畸变可能导致能隙的形成或变化。例如,一些原子的位移可能导致声子频谱中出现新的能隙。
- 非谐效应的增强:结构畸变通常会增强非谐效应,即声子模式之间的相互作用,这会影响声子的寿命和热传导特性。

比如在 2021 年,美国加州大学尔湾分校材料科学与工程系潘晓晴教授课题组和物理天文系武汝前教授课题组合作在 Nature 发表了“Single-defect phonons imaged by electron microscopy”一文。
该工作利用空间分辨、动量分辨和能量分辨的电子能量损失谱研究材料中单个缺陷的局域缺陷声子谱。
该研究发现在碳化硅材料中广泛存在的层错缺陷会形成缺陷声子态,将会造成横波声学支(transverse acoustic phonon, TA)能量降低 3.8 meV ,同时对比块体本征声子模,其态密度有显著的增强。2

声子谱的态密度¶
声子谱的态密度(Density of States, DOS)用于描述在固体物理学中声子(晶格振动的量子)的分布情况。
定义:态密度是每单位能量范围内可用的声子态的数量。它告诉我们在某个特定能量水平上有多少声子模式可以被激发。
特点:
- 在低频(长波长)极限,声子态密度通常呈线性增加,与声学模式相关。
- 在高频(短波长)极限,态密度通常达到峰值后迅速下降,与光学模式相关。
声子谱与电子态密度的对比:类似于电子态密度,声子态密度也是研究固体物理特性的一个关键参数,但它们关注的是声子(晶格振动的量子化模式)而非电子。
态密度是连接微观物理与宏观物理学性质的桥梁,通过它,我们能更好地理解和预测固体材料的各种物理行为。
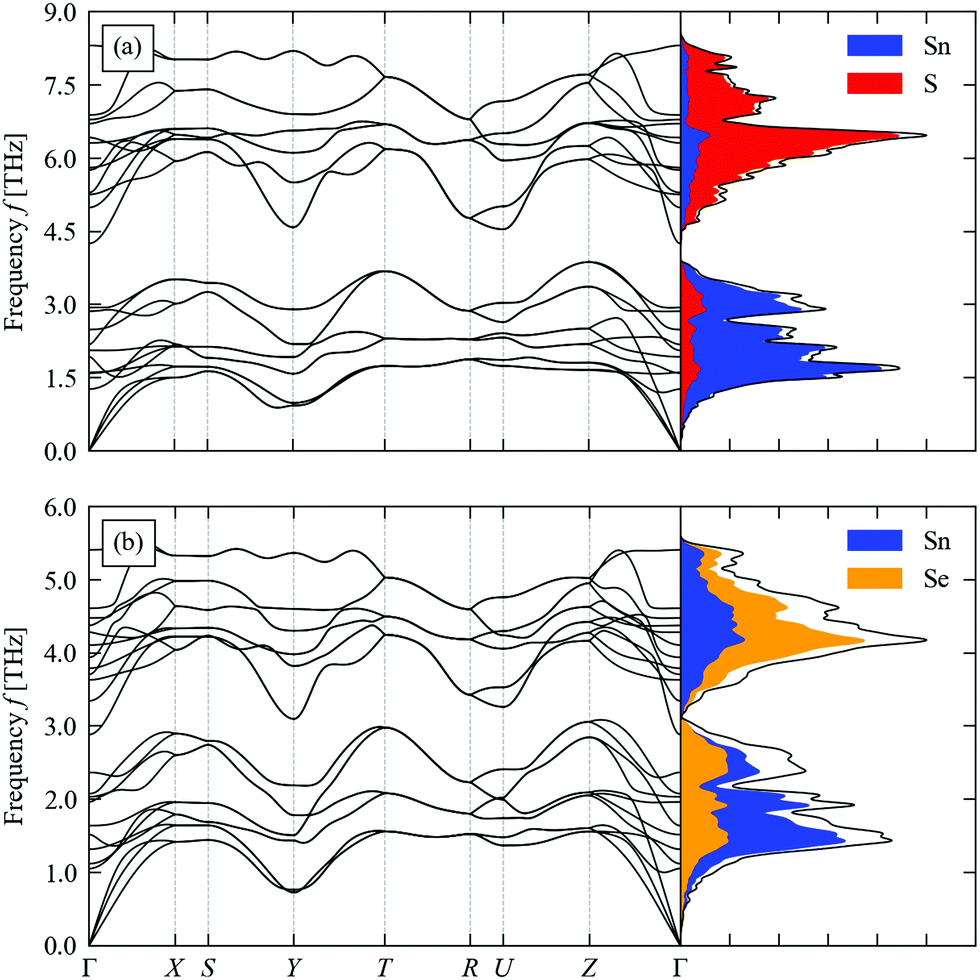
声子谱的态密度有什么用?
对于一个物理体系,能量分布很重要。
能量分布决定了体系的状态或者材料的性能。
统计力学中,我们常会遇到配分函数,配分函数的实质就是能量的分布。
能量分配方式 $\Rightarrow $ 配分函数 $\Rightarrow $ 体系的熵和自由能 $\Rightarrow $ 体系的状态
态密度实际上也就对应着能量分布,有了态密度,我们就可以根据统计力学得到想要的热力学量(宏观性质)。3
另外,通过测量声子光谱,可以得到声子态密度的实验数据。这对于验证材料的理论模型和理解材料的基本物理特性非常重要。
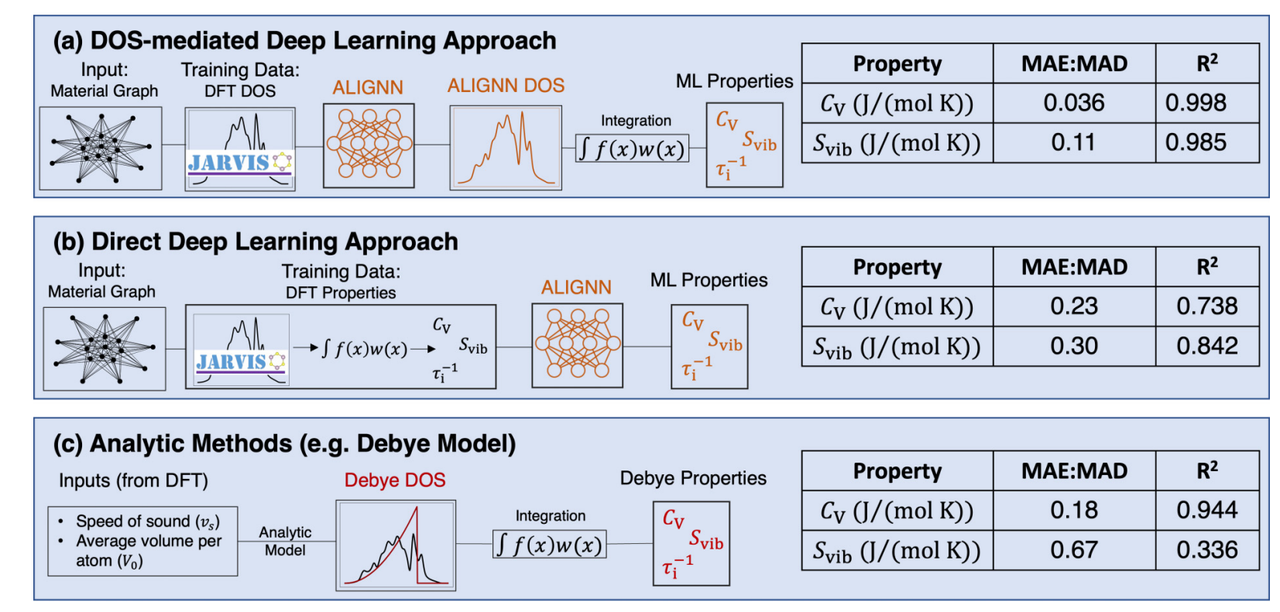
下面这篇文章介绍了一个用于预测声子谱的态密度及其衍生的热力学和热物性的原子线图神经网络(ALIGNN)模型。该模型基于超过 14000 个声子光谱的数据库进行训练,能够有效地分类动力学稳定性,并准确预测了基于 DOS 的热力学相关性质(包括热容)。4
能带图中的 k 点和声子谱中的 k 点一样吗?
能带图中的 k 点和声子谱中的 k 点本质上是相同的概念,但它们应用于不同的物理情境。在这两种情况下, k 点都表示晶体动量空间(或布里渊区)中的一个点,但它们分别关联到电子的能量状态和晶格振动模式。
能带图中的 k 点:
- 在能带理论中, k 点表示电子的波矢,它是电子量子态的特征。
- 能带图展示了电子的能量与其波矢( k 值)之间的关系,用于描述固体中电子的能量分布。
声子谱中的 k 点:
- 在声子谱中, k 点也表示波矢,但它是晶格振动模式或声子的特征。
- 声子谱显示了晶格振动模式的能量(或频率)与其相应的波矢( k 值)之间的关系。
综上,尽管它们的物理含义略有不同(一个关于电子,另一个关于晶格振动),但在数学框架下, k 点的概念是一致的。
