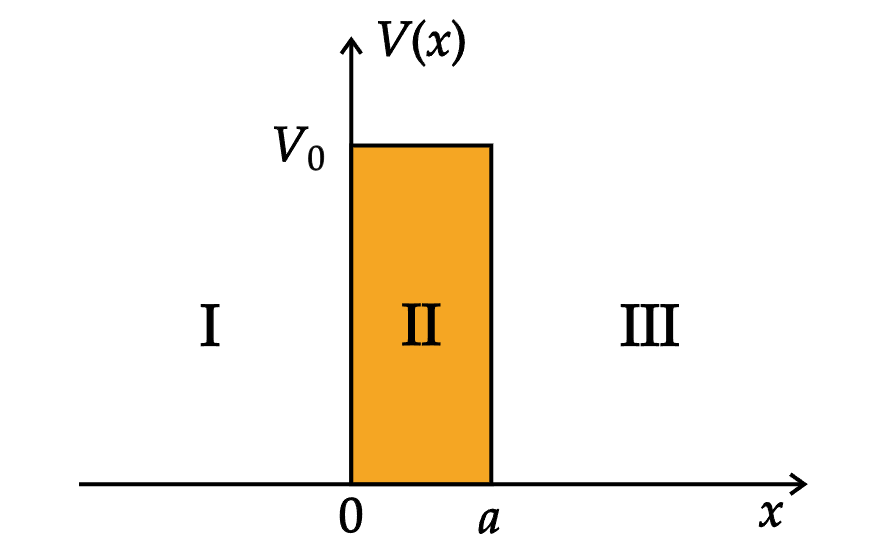
一维方势垒

在经典力学里，一维方势垒问题会设定一个粒子，从方势垒的左边，往方势垒移动。如果，粒子的能量大于方势垒的势能。则这粒子，在经过方势垒的时候，因为动能的转换为势能，速度会降低，但方向不会改变。当移动至方势垒外时，速度又会回复至原本值。假若，粒子的能量小于方势垒的势能，则在与方势垒弹性碰撞之后，这粒子会改变方向，以同样的速率，往回移动。粒子绝对无法存在于方势垒内或越过势垒。

在量子力学里，粒子的量子行为，是取决于其波函数。由于粒子没有被方势垒束缚，粒子的能量不是离散能量谱的特征值，而是大于 0 的任意值，因此不需要求算粒子的能量。在这里，主要研究的是粒子的一维散射 。这是一个很有意思的领域。

如果，粒子的能量大于方势垒的势能。由于往方势垒传播的波函数，并不是完全地透射过方势垒，仍旧有一部分反射回来。所以，反射的概率幅大于 0 ，粒子被反射回来的概率大于 0 。

如果，粒子的能量小于方势垒的势能，虽然波函数会呈指数地递减，在方势垒内，概率幅仍旧大于 0 。所以，这粒子存在于方势垒内的概率大于 0。不止这样，概率幅在方势垒外的另一边也大于 0 。

如果，方势垒的位势并不是远远的超过粒子的能量，方势垒的垒宽也并不很宽，则粒子穿越位势垒的概率会是很显著的，称这效应为量子隧穿效应。透射的可能性，称为透射系数；反射的可能性，则称为反射系数。

考虑一个能量为 \(E\) 的粒子沿 \(x\) 轴正方向从左向势垒运动。

势能函数为：

\[V(x)=\left\{\begin{array}{lc}V_{0} & (0<x<a) \\0 & (x \leq 0, \quad x \geq a)\end{array}\right.\]

一维方势垒

经典力学：若 \(E\) 小于势垒高度，粒子将被弹回，不能穿透势垒。若 \(E\) 大于势垒高度，粒子能够穿透势垒。

量子力学：无论 \(E\) 大于还是小于势垒高度，粒子均有一定的几率穿透势垒，也有一定的几率弹回（反射）。

量子隧道效应（Quantum tunneling effect）：能量低于势垒高度的粒子有一定几率穿透势垒的现象。

体系的哈密顿算符：\(\displaystyle\hat{H}=-\frac{\hbar^{2}}{2 m} \frac{d^{2}}{d x^{2}}+V(x)\)

薛定谔方程：\(\hat{H} \psi=E \psi\)

\(E\) 小于 \(V_0\) 的情形

分区求解

I 区：\(\displaystyle\psi^{\prime \prime}+\frac{2 m E}{\hbar^{2}} \psi=0\)

II 区：\(\displaystyle\psi^{\prime \prime}-\frac{2 m (V_0-E)}{\hbar^{2}} \psi=0\)

III 区：\(\displaystyle\psi^{\prime \prime}+\frac{2 m E}{\hbar^{2}} \psi=0\)

其解为：\(\psi(x) \sim e^{i k_{1} x}, e^{-i k_{1} x}\)

其中：\(\displaystyle k_{1}=\frac{\sqrt{2 m E}}{\hbar}\)

\(\psi(x) \sim e^{i k_{1} x}\) 为沿 \(x\) 轴正方向运动的粒子的波函数。

\(\psi(x) \sim e^{-i k_{1} x}\) 为沿 \(x\) 轴负方向运动的粒子的波函数。

在每个区域内，我们可以先假设，既有沿 \(x\) 轴正方向运动的粒子也有沿 \(x\) 轴负方向运动的粒子。

\[\begin{cases}\psi_{I}(x)=A e^{i k_{1} x}+A' e^{-i k_{1} x} ,&\quad x<0 \\\psi_{II}(x)=B e^{ k_{2} x}+B' e^{- k_{2} x} ,&\quad 0<x<a \\\psi_{III}(x)=C e^{i k_{1} x}+C' e^{-i k_{1} x} ,&\quad a<x \end{cases}\]

之后，我们可以根据具体的情况忽略掉一些参数。

如果粒子从左侧入射，在 I 区，既有入射波 \(\exp \left(i k_{1} x\right)\) ，也有反射波 \(\exp \left(-i k_{1} x\right)\) ，而在 III 区，只有透射波 \(\exp \left(i k_{1} x\right)\) 。

于是：

\[\begin{cases}\psi_{I}(x)=A e^{i k_{1} x}+A' e^{-i k_{1} x} ,&\quad x<0 \\\psi_{II}(x)=B e^{ k_{2} x}+B' e^{- k_{2} x} ,&\quad 0<x<a \\\psi_{III}(x)=C e^{i k_{1} x} ,&\quad a<x \end{cases}\]

在 II 区（势垒内部，为经典禁区）：

\[\displaystyle \psi^{\prime \prime}-\frac{2 m}{\hbar^{2}}\left(V_{0}-E\right) \psi=0 \Longrightarrow \psi^{\prime \prime}-k_{2}^{2} \psi=0\]

其中 \(\displaystyle k_{2}=\frac{\sqrt{2 m\left(V_{0}-E\right)}}{\hbar}\) ；

因为 \(E<V_{0}\) ，所以 \(\displaystyle k_{2}=\frac{\sqrt{2 m\left(V_{0}-E\right)}}{\hbar}>0\) 。

解的系数由波函数及其一阶导数在边界的连续性确定：

I 区：\(\psi_{I}(x)=A \exp \left(i k_{1} x\right)+A^{\prime} \exp \left(-i k_{1} x\right)\)

II 区：\(\psi_{I I}(x)=B \exp \left(k_{2} x\right)+B^{\prime} \exp \left(-k_{2} x\right)\)

当 \(x=0\) 的时候，因为：

\[ \begin{array}{c}\psi_{I}(0)=\psi_{I I}(0)\\\psi_{I}{ }^{\prime}(0)=\psi_{I I}{ }^{\prime}(0)\\\end{array} \]

所以：

\[ \begin{array}{ll}A+A^{\prime}&=B+B^{\prime}\\i k_{1}\left(A-A^{\prime}\right)&=k_{2}\left(B-B^{\prime}\right)\\\end{array} \]

联立上述两式，我们可以解得：

\[ \begin{array}{ll}\displaystyle B&\displaystyle=\frac{1}{2 k_{2}}\left[A\left(k_{2}+i k_{1}\right)+A^{\prime}\left(k_{2}-i k_{1}\right)\right]\\\displaystyle B^{\prime}&\displaystyle=\frac{1}{2 k_{2}}\left[A\left(k_{2}-i k_{1}\right)+A^{\prime}\left(k_{2}+i k_{1}\right)\right]\\\end{array} \]

II 区： \(\psi_{I I}(x)=B \exp \left(k_{2} x\right)+B^{\prime} \exp \left(-k_{2} x\right)\)

III 区： \(\psi_{I I I}(x)=C \exp \left(i k_{1} x\right)\)

当 \(x=a\) 的时候，因为：

\[ \begin{array}{c}\psi_{I I}(a)=\psi_{I I I}(a)\\\psi_{I I}{ }^{\prime}(a)=\psi_{I I I}{ }^{\prime}(a)\\\end{array} \]

我们可以得到：

\[ \begin{array}{ll} B \exp \left(k_{2} a\right)+B^{\prime} \exp \left(-k_{2} a\right)&=C \exp \left(i k_{1} a\right)\\ k_{2}\left[B \exp \left(k_{2} a\right)-B^{\prime} \exp \left(-k_{2} a\right)\right]&=i k_{1} C \exp \left(i k_{1} a\right) \end{array} \]

联立上述两式，我们可以解得：

\[ \begin{array}{ll} \displaystyle B&\displaystyle=\frac{C}{2 k_{2}}\left[k_{2}+i k_{1}\right] \exp \left(i k_{1} a-k_{2} a\right)\\ \displaystyle B^{\prime}&\displaystyle=\frac{C}{2 k_{2}}\left[k_{2}-i k_{1}\right] \exp \left(i k_{1} a+k_{2} a\right) \end{array} \]

I 区和 II 区解得的关系：

\[ \begin{array}{ll} \displaystyle B&\displaystyle=\frac{1}{2 k_{2}}\left[A\left(k_{2}+i k_{1}\right)+A^{\prime}\left(k_{2}-i k_{1}\right)\right]\\ \displaystyle B^{\prime}&\displaystyle=\frac{1}{2 k_{2}}\left[A\left(k_{2}-i k_{1}\right)+A^{\prime}\left(k_{2}+i k_{1}\right)\right] \end{array} \]

II 区和 III 区解得的关系：

\[ \begin{array}{ll} \displaystyle B&\displaystyle=\frac{C}{2 k_{2}}\left[k_{2}+i k_{1}\right] \exp \left(i k_{1} a-k_{2} a\right)\\ \displaystyle B^{\prime}&\displaystyle=\frac{C}{2 k_{2}}\left[k_{2}-i k_{1}\right] \exp \left(i k_{1} a+k_{2} a\right) \end{array} \]

联立上述四式，我们可以解得：

\[ \begin{array}{ll} A\left(k_{2}+i k_{1}\right)+A^{\prime}\left(k_{2}-i k_{1}\right)&=C\left[k_{2}+i k_{1}\right] \exp \left(i k_{1} a-k_{2} a\right)\\ A\left(k_{2}-i k_{1}\right)+A^{\prime}\left(k_{2}+i k_{1}\right)&=C\left[k_{2}-i k_{1}\right] \exp \left(i k_{1} a+k_{2} a\right) \end{array} \]

整理上述两式，我们可以解得：

\[ \begin{array}{ll} A^{\prime}\left(k_{2}-i k_{1}\right)&=\left[k_{2}+i k_{1}\right]\left[C \exp \left(i k_{1} a-k_{2} a\right)-A\right]\\ A^{\prime}\left(k_{2}+i k_{1}\right)&=\left[k_{2}-i k_{1}\right]\left[C \exp \left(i k_{1} a+k_{2} a\right)-A\right] \end{array} \]

联立上述两式，我们可以解得：

\[\left[k_{2}+i k_{1}\right]^{2}\left[C \exp \left(i k_{1} a-k_{2} a\right)-A\right]=\left[k_{2}-i k_{1}\right]^{2}\left[C \exp \left(i k_{1} a+k_{2} a\right)-A\right]\]

移项：

\[C \exp \left(i k_{1} a\right)\left[\left(k_{2}+i k_{1}\right)^{2} \cdot \exp \left(-k_{2} a\right)-\left(k_{2}-i k_{1}\right)^{2} \cdot \exp \left(k_{2} a\right)\right]=4 i k_{1} k_{2} \cdot A\]

故有：

\[\displaystyle \frac{C}{A} \exp \left(i k_{1} a\right)=\frac{4 i k_{1} k_{2}}{\left(k_{2}+i k_{1}\right)^{2} \cdot \exp \left(-k_{2} a\right)-\left(k_{2}-i k_{1}\right)^{2} \cdot \exp \left(k_{2} a\right)}\]

利用数学公式：

\[ \begin{array}{c} \displaystyle \operatorname{sh} x\displaystyle=\frac{e^{x}-e^{-x}}{2}\\ \displaystyle \operatorname{ch} x\displaystyle=\frac{e^{x}+e^{-x}}{2}\\ \exp \left(-k_{2} a\right)=\operatorname{ch} k_{2} a-\operatorname{sh} k_{2} a\\ \exp \left(k_{2} a\right)=\operatorname{ch} k_{2} a+\operatorname{sh} k_{2} a\\ \operatorname{ch}^2 k_{2} a-\operatorname{sh}^2 k_{2} a=1 \end{array} \]

所以：

\[\begin{array}{ll}{\left(k_{2}^{2}-k_{1}^{2}+2 i k_{1} k_{2}\right)\left(\operatorname{ch} k_{2} a-\operatorname{sh} k_{2} a\right)} -\left(k_{2}^{2}-k_{1}^{2}-2 i k_{1} k_{2}\right)\left(\operatorname{ch} k_{2} a+\operatorname{sh} k_{2} a\right) \\=\left(k_{2}^{2}-k_{1}^{2}+2 i k_{1} k_{2}\right)exp(-k_2a)-\left(k_{2}^{2}-k_{1}^{2}-2 i k_{1} k_{2}\right)exp(k_2a)\\=\left(k_{2}^{2}-k_{1}^{2}\right)[exp(-k_2a)-exp(k_2a)]+2ik_{1} k_{2}[exp(-k_2a)+exp(k_2a)]\\=-2\left(k_{2}^{2}-k_{1}^{2}\right) \operatorname{sh} k_{2} a+4 i k_{1} k_{2} \operatorname{ch} k_{2} a\\\end{array}\]

将上式带入，我们可以得到：

\[\displaystyle \frac{C}{A} \exp \left(i k_{1} a\right)=\frac{2 i k_{1} k_{2}}{\left[k_{1}^{2}-k_{2}^{2}\right] \cdot \operatorname{sh} k_{2} a+2 i\left(k_{1} k_{2}\right) \operatorname{ch} k_{2} a}\]

利用公式 \(\displaystyle \left|\frac{i b}{c+i d}\right|^{2}=\frac{b^{2}}{c^{2}+d^{2}}\) 和几率流密度 \(\displaystyle J=-\frac{i \hbar}{2 m}\left(\psi^{*} \nabla \psi-\psi \nabla \psi^{*}\right)\) ，我们可以得到：

透射系数：\(\displaystyle T=\left|\frac{C}{A}\right|^{2}=\frac{4 k_{1}^{2} k_{2}^{2}}{\left[k_{1}^{2}-k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2} \operatorname{ch}^{2} k_{2} a}\)

因为透射系数的分母还可以写成：

\[\begin{array}{ll}\left[k_{1}^{2}-k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2} \operatorname{ch}^{2} k_{2} a\\=\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2} \operatorname{ch}^{2} k_{2} a-4 k_{1}^{2} k_{2}^{2} \operatorname{sh}^{2} k_{2}a\\=\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2}\end{array}\]

所以透射系数还可以写为：

\[\displaystyle T=\left|\frac{C}{A}\right|^{2}=\frac{4 k_{1}^{2} k_{2}^{2}}{\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2} }\]

根据透射系数和反射系数的关系 \(T+R=1\) ，我们可以得到反射系数。

反射系数： \(\displaystyle R=\left|\frac{A^{\prime}}{A}\right|^{2}=\frac{\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a}{\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2} }\)

结果分析与讨论| \(E<V_{0}\) 情况下

结论一

量子隧道效应（Quantum tunneling effect）

图片链接

经典力学 VS 量子力学

按照经典力学的观念，\(E<V_{0}\) 情况下粒子是无法穿过势垒的。

但是根据上述的推导，我们发现根据量子力学的理论，即使 \(E<V_{0}\)，粒子也有一定的几率穿透势垒，因为透射系数不为零。

\[ \begin{array}{ll} \displaystyle T&\displaystyle=\frac{4 k_{1}^{2} k_{2}^{2}}{\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2}}>0\\ \displaystyle k_{1}&\displaystyle=\frac{\sqrt{2 m E}}{\hbar}\\ \displaystyle k_{2}&\displaystyle=\frac{\sqrt{2 m\left(V_{0}-E\right)}}{\hbar} \end{array} \]

我们称上述现象为量子隧道效应（Quantum tunneling effect）。

结论二

在没有外部粒子输入或输出的情况下，方势垒中的总粒子数是守恒的。这意味着，尽管单个粒子的位置可能不确定，整体粒子数在势垒内是恒定的。这一点可以从波函数的归一化条件中得出，即整个空间中波函数的绝对值平方的积分（即找到粒子的总概率）等于 1 。

当粒子遇到方势垒时，它可以被反射回来，也可以穿过势垒（量子穿隧效应）。这两种情况的概率之和等于 1 ，这也是粒子数守恒的表现。即使部分粒子穿过势垒，总粒子数（反射和透射粒子数之和）仍然保持不变。

粒子数守恒：\(R+T=1\)

结论三

当 \(k_{2} a \gg1\) 时，对应于高且宽的势垒；

由于：\(\displaystyle T=\frac{4 k_{1}^{2} k_{2}^{2}}{\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2}}\)

根据近似公式：\(\displaystyle \operatorname{sh} k_{2} a \approx \frac{1}{2} \exp \left(k_{2} a\right)\gg 1\)

我们可以得到：\(\displaystyle T \approx \frac{16 k_{1}^{2} k_{2}^{2}}{\left[k_{1}^{2}+k_{2}^{2}\right]^{2}} \exp \left(-2 k_{2} a\right)\)

由于：

\[ \begin{array}{ll} \displaystyle k_{1}&\displaystyle=\frac{\sqrt{2 m E}}{\hbar}\\ \displaystyle k_{2}&\displaystyle=\frac{\sqrt{2 m\left(V_{0}-E\right)}}{\hbar} \end{array} \]

我们可以知道：

\[ \begin{array}{ll} \displaystyle k_{1}^{2} k_{2}^{2}&\displaystyle=\left(\frac{2m}{\hbar^{2}}\right)^{2} E\left(V_{0}-E\right)\\ \displaystyle k_{1}^{2}+k_{2}^{2}&\displaystyle=\frac{2mV_{0}}{\hbar^{2}} \end{array} \]

所以，我们可以得到透射系数的近似关系：

\[\displaystyle T \approx \frac{16 E\left(V_{0}-E\right)}{V_{0}^{2}} \exp \left(-\frac{2 a}{\hbar} \sqrt{2 m\left(V_{0}-E\right)}\right)\]

结论四

当 \(k_{2} a \to0\) 时，对应于薄的势垒；

\[T=\left|\frac{C}{A}\right|^{2}=\frac{4 k_{1}^{2} k_{2}^{2}}{\left[k_{1}^{2}+k_{2}^{2}\right]^{2} \operatorname{sh}^{2} k_{2} a+4 k_{1}^{2} k_{2}^{2} }\]

上式也科学写为：

\[\displaystyle T=\left[1+\left(\frac{k_{1}^{2}+k_{2}^{2}}{2 k_{1} k_{2}}\right)^{2} \mathrm{sh} ^{2}\left(2 k_{2} a\right)\right]^{-1}\]

因为 \(k_{2} a \to0\) ，所以透射系数可以近似为：

\[T \sim e^{-2 k_{2} a}\]

结论五

对于任意形状势垒 \(V(x)\) ，势垒的某些地方总是大于粒子的动能 \(V(x)>E\) 。

我们可以将它们细分成不同方势垒，整体就是分成的不同方势垒的叠加。

比如在 \(x\) 处的 \(k\) 值为：\(\displaystyle k(x)=\frac{\sqrt{2 m\left(V(x)-E\right)}}{\hbar}\)

图片链接

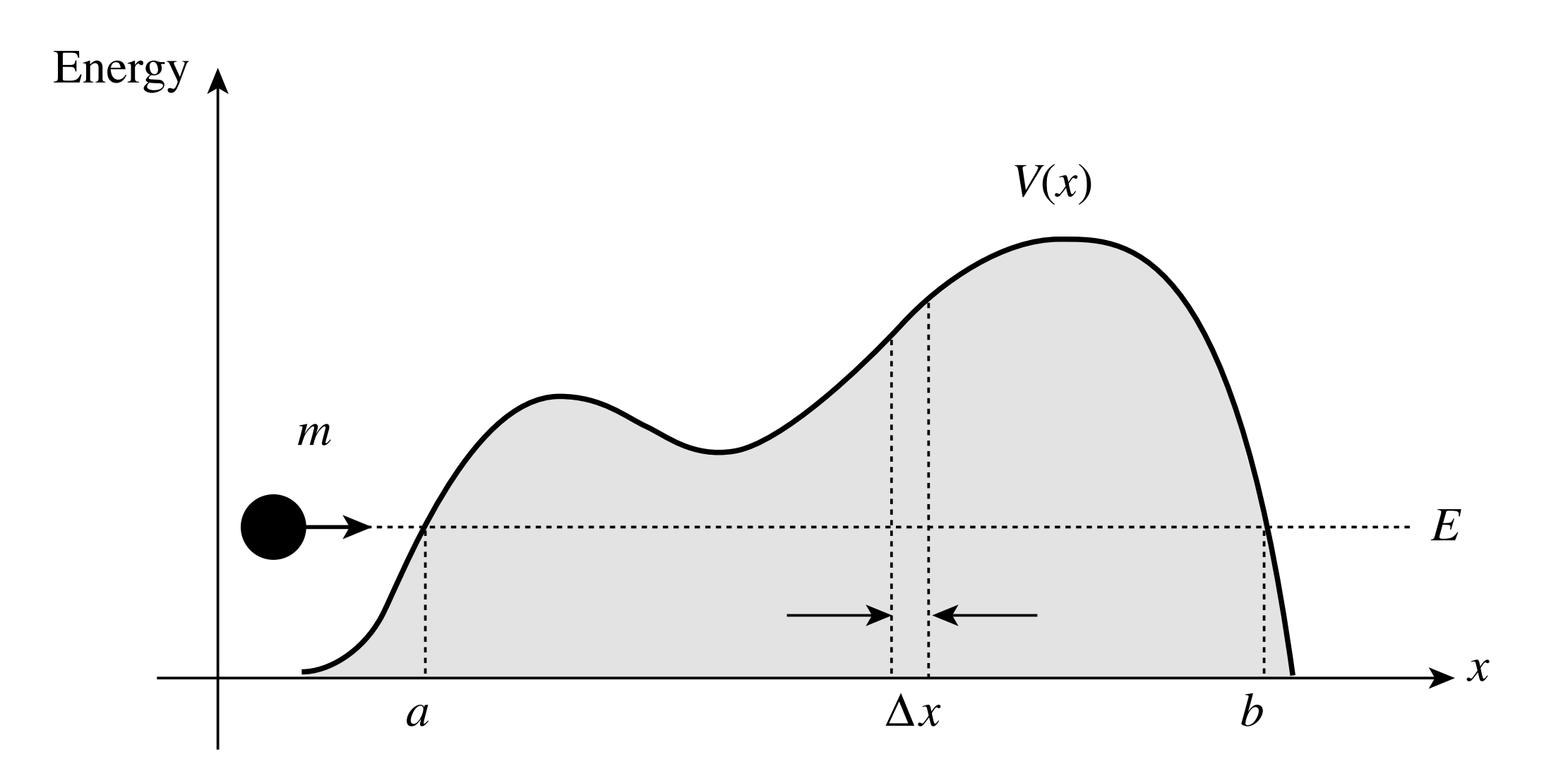
总体的穿透系数就是细分成的不同方势垒的穿透系数的乘积：

\[\begin{array}{ll}T&=T_{1} T_{2} \cdots T_{N} \\&=T_{0}e^{-2 k_{1}\Delta x }e^{-2 k_{2} \Delta x}\cdots e^{-2 k_{N} \Delta x}\\&=T_{0}e^{-2 (k_{1}+k_{2}+\cdots+k_{N})\Delta x }\\&\displaystyle=T_{0}\exp\left(\displaystyle-2 \sum_1^nk_n\Delta x \right)\\&\displaystyle =T_{0} \exp \left(-\frac{2}{\hbar} \int_{a}^{b} \sqrt{2 m(V(x)-E)} d x\right)\end{array}\]

\(E\)大于 \(V_0\) 的情形

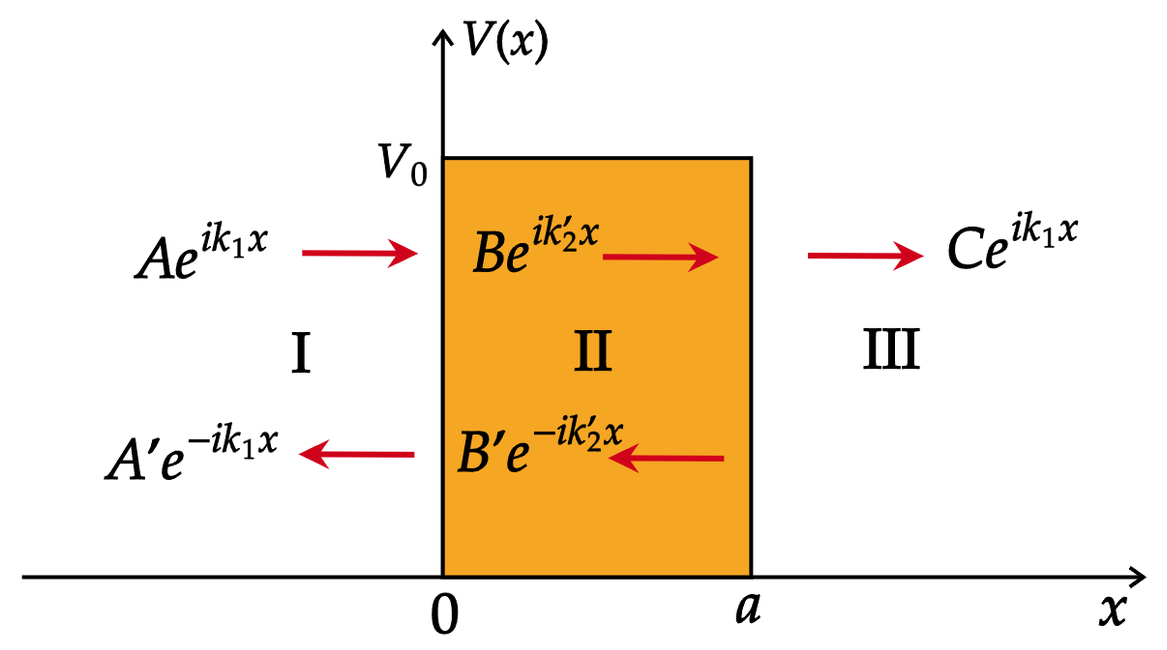
I 区：\(\displaystyle \psi^{\prime \prime}+\frac{2 m E}{\hbar^{2}} \psi=0\)

II 区：\(\displaystyle \psi^{\prime \prime}+\frac{2 m}{\hbar^{2}}\left(E-V_{0}\right) \psi=0\)

III 区：\(\displaystyle \psi^{\prime \prime}+\frac{2 m E}{\hbar^{2}} \psi=0\)

其解为：

\[\begin{cases}\psi_{I}(x)=A e^{i k_{1} x}+A' e^{-i k_{1} x} ,&\quad x<0 \\\psi_{II}(x)=B e^{i k'_{2} x}+B' e^{- ik'_{2} x} ,&\quad 0<x<a \\\psi_{III}(x)=C e^{i k_{1} x} ,&\quad a<x \end{cases}\]

\[ \begin{array}{ll} \displaystyle k_{1}&\displaystyle=\frac{\sqrt{2 m E}}{\hbar}\\ \displaystyle k_{2}^{\prime}&\displaystyle=\frac{\sqrt{2 m\left(E-V_{0}\right)}}{\hbar} \end{array} \]

系数由边界条件确定：

\[ \begin{array}{cc} \psi_{I}(0)=\psi_{I I}(0)\\ \psi_{I}{ }^{\prime}(0)=\psi_{I I}{ }^{\prime}(0)\\ \psi_{I I}(a)=\psi_{I I I}(a)\\ \psi_{I I}{ }^{\prime}(a)=\psi_{I I I}{ }^{\prime}(a) \end{array} \]

联立上述四式，我们可以解得透射系数和反射系数。

利用前面的结果（\(E\) 小于 \(V_0\) 的情形），我们也可以解出：

\[\displaystyle i k_{2}{ }^{\prime} \rightarrow k_{2} \Longrightarrow \frac{C}{A} \exp \left(i k_{1} a\right)=\frac{2 i k_{1} k_{2}}{\left[k_{1}{ }^{2}-k_{2}{ }^{2}\right] \cdot \operatorname{sh} k_{2} a+2 i\left(k_{1} k_{2}\right) \operatorname{ch} k_{2} a}\]

我们可以得到：

\[\displaystyle \frac{C}{A} \exp \left(i k_{1} a\right)=\frac{-2 k_{1} k_{2}{ }^{\prime}}{\left[k_{1}{ }^{2}+k_{2}{ }^{\prime 2}\right] \cdot \operatorname{sh}\left(i k_{2}{ }^{\prime} a\right)-2\left(k_{1} k_{2}{ }^{\prime}\right) \operatorname{ch}\left(i k_{2}{ }^{\prime} a\right)}\]

又因为：

\[ \begin{array}{ll} \displaystyle \operatorname{sh}(i x)&\displaystyle=\frac{\left(e^{i x}-e^{-i x}\right)}{2}=i \sin x\\ \displaystyle \operatorname{ch}(i x)&\displaystyle=\frac{\left(e^{i x}+e^{-i x}\right)}{2}=\cos x \end{array} \]

我们可以得到：

\[\displaystyle \frac{C}{A} \exp \left(i k_{1} a\right)=\frac{-2 k_{1} k_{2}{ }^{\prime}}{i\left[k_{1}{ }^{2}+k_{2}{ }^{\prime 2}\right] \cdot \sin k_{2}{ }^{\prime} a-2\left(k_{1} k_{2}{ }^{\prime}\right) \cos k_{2}{ }^{\prime} a}\]

透射系数：\(\displaystyle T=\left|\frac{C}{A}\right|^{2}=\frac{4 k_{1}^{2} k_{2}^{\prime 2}}{\left[k_{1}^{2}-k_{2}^{\prime 2}\right]^{2} \sin ^{2} k_{2}^{\prime} a+4 k_{1}^{2} k_{2}^{\prime 2}}\)

反射系数： \(\displaystyle R=\left|\frac{A^{\prime}}{A}\right|^{2}=\frac{\left[k_{1}^{2}-k_{2}^{\prime 2}\right]^{2} \sin ^{2} k_{2}^{\prime} a}{\left[k_{1}^{2}-k_{2}^{\prime 2}\right]^{2} \sin ^{2} k_{2}^{\prime} a+4 k_{1}^{2} k_{2}^{\prime 2}}\)

其中：

\[ \begin{array}{ll} \displaystyle k_{1}&\displaystyle=\frac{\sqrt{2 m E}}{\hbar}\\ \displaystyle k_{2}{ }^{\prime}&\displaystyle=\frac{\sqrt{2 m\left(E-V_{0}\right)}}{\hbar} \end{array} \]

结果分析与讨论| \(E>V_{0}\) 情况下

结论一

在 \(E>V_{0}\) 的情况下，粒子一般也不能百分之百的穿透势垒。

透射系数：\(\displaystyle T=\left|\frac{C}{A}\right|^{2}=\frac{4 k_{1}^{2} k_{2}^{\prime 2}}{\left[k_{1}^{2}-k_{2}^{\prime 2}\right]^{2} \sin ^{2} k_{2}^{\prime} a+4 k_{1}^{2} k_{2}^{\prime 2}}\)

反射系数：\(\displaystyle R=\left|\frac{A^{\prime}}{A}\right|^{2}=\frac{\left[k_{1}^{2}-k_{2}^{\prime 2}\right]^{2} \sin ^{2} k_{2}^{\prime} a}{\left[k_{1}^{2}-k_{2}^{\prime 2}\right]^{2} \sin ^{2} k_{2}^{\prime} a+4 k_{1}^{2} k_{2}^{\prime 2}}\)

根据我们推导出的透射系数和反射系数，我们可以发现粒子也有一定的几率被反射。

结论二

透射系数：\(\displaystyle T=\left|\frac{C}{A}\right|^{2}=\frac{4 k_{1}^{2} k_{2}^{\prime 2}}{\left[k_{1}^{2}-k_{2}^{\prime 2}\right]^{2} \sin ^{2} k_{2}^{\prime} a+4 k_{1}^{2} k_{2}^{\prime 2}}\)

根据透射系数的公式，我们可以发现，在某些情况下，粒子是可以百分之百穿透势垒的。

情况一：\(k_{2}^{\prime}=k_{1}\)，也就是不存在势垒的时候，粒子会百分之百的穿过势垒。

情况二：\(\mathrm{sin}^2k'_2a=0\)，也就是 \(\displaystyle k_{2}^{\prime} a=\frac{a \sqrt{2 m\left(E-V_{0}\right)}}{\hbar}=n \pi\) 的时候。

第二种情况，我们称为共振隧穿（Resonant tunneling）现象。

共振隧穿（Resonant Tunneling）是量子力学中的一个现象，它发生在粒子穿越一个或多个势垒的过程中。这一现象的关键在于粒子可以在特定条件下，通过量子隧穿效应，以较高的概率穿越势垒。

对应的能级为共振能级：\(\displaystyle E_{n}=\frac{\pi^{2} \hbar^{2}}{2 m a^{2}} n^{2}+V_{0}\)

量子隧道效应的应用

质子转移

图片链接

"质子转移"（Proton transfer）是一个化学过程，涉及到质子（氢原子核）从一个分子或原子转移到另一个分子或原子。这是酸和碱反应的基本机制，因为酸是质子的供体，而碱是质子的受体。

在质子转移过程中，一个质子从酸性分子转移到碱性分子。这个过程通常发生在两个分子之间的特定位置，这些位置具有相对较高的电子密度（如氧原子或氮原子上），从而有能力吸引并暂时保留质子。

这个概念在很多化学反应中都非常重要，包括在溶液化学、酶催化反应以及能量传输过程中。例如，水的自我电离就是一个质子转移过程的例子，其中一个水分子（作为酸）将一个质子转移到另一个水分子（作为碱），形成一个氢离子（H⁺）和一个氢氧根离子（OH⁻）。

从量子力学的角度来解释质子转移，我们需要考虑电子的波函数、能量隧穿效应以及量子态的叠加。在量子尺度上，粒子（如电子和质子）的行为不再遵循经典物理学的定律，而是遵循量子力学的原理。

1. 电子的波函数和重叠： 在量子力学中，电子不是以粒子的形式存在于一个特定位置，而是通过波函数来描述，这个波函数表示了电子存在于某处的概率。在质子转移的过程中，当两个原子或分子接近时，它们的电子云（电子波函数的空间分布）会相互重叠。这种重叠改变了电子的能量状态，从而影响原子和分子之间的化学键和反应性。
2. 量子隧道效应： 在量子力学中，粒子（如质子）有可能穿过看似不可能穿越的势垒，这称为量子隧穿。即使在经典物理学中质子不具有足够的能量跨越两个分子之间的势垒，量子隧穿仍然允许质子从一个分子转移到另一个分子。
3. 量子态的叠加： 在质子转移过程中，质子的具体位置不是确定的，而是以一种量子叠加的状态存在，即同时存在于供体和受体分子上。只有在进行测量或发生特定的化学反应时，质子的位置才会“坍缩”到特定的状态。
4. 氢键的量子性质： 在形成氢键（如水分子之间的氢键）时，质子的位置和行为也是由量子力学支配的。氢键中的质子可以在两个电子云间共享，这种共享在一定程度上是由量子力学效应驱动的。

总体而言，质子转移现象在量子力学框架下可以被理解为电子波函数的重叠、量子隧穿效应和量子态叠加的结果。这些量子效应使得质子在不同的化学环境中可以以非经典的方式移动和反应。

\(\alpha\) 衰变

“\(\alpha\)衰变”（Alpha decay）是一种放射性衰变过程，其中一个原子核释放出一个 \(\alpha\) 粒子。在这个过程中，原子核失去两个质子和两个中子，这四个粒子共同构成了一个 \(\alpha\) 粒子，它实际上就是一个 \(\bf^4_2He\) 。由于失去了这些粒子，原子的原子序（即质子数）减少了两个，而质量数（即质子和中子的总数）减少了四个。

图片链接

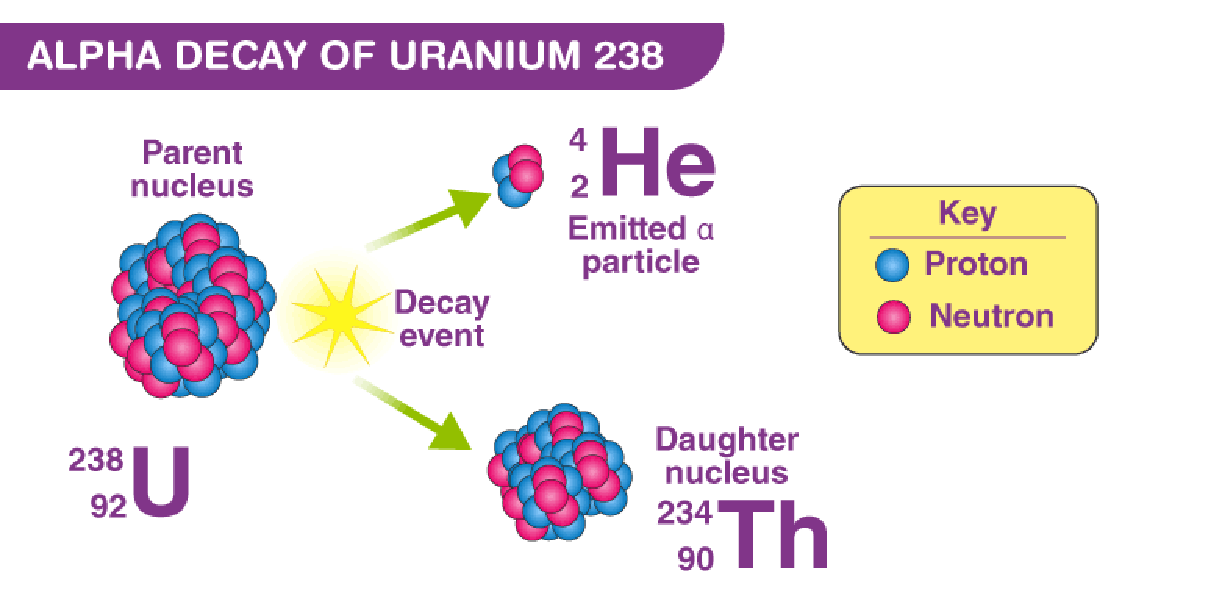
例如，当 \(\bf ^{238}_{92}U\) 经历 \(\alpha\) 衰变时，它会失去一个 \(\alpha\) 粒子，变成 \(\bf^{234}_{90}Th\)：

\[\bf ^{238}_{92}U \rightarrow \bf^{234}_{90}Th+\bf^4_2He\]

这个过程减少了原子核中的质子数和中子数，从而改变了元素的类型。\(\alpha\) 衰变通常发生在重元素中，如铀和钍，这些元素的原子核足够大，能够释放 \(\alpha\) 粒子。

图片链接

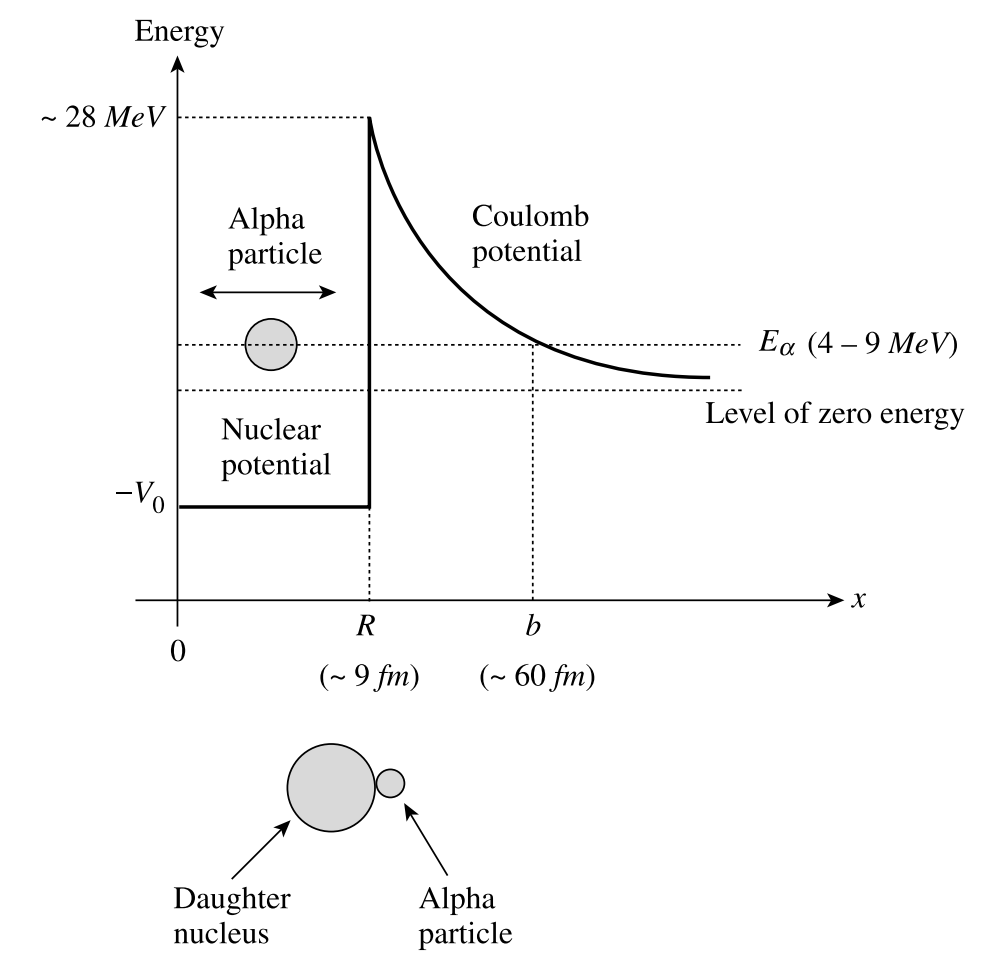
\(\alpha\) 衰变可以通过量子隧道效应来解释。在经典物理学中，\(\alpha\) 粒子被原子核的势垒所囚禁，因为它没有足够的能量来克服这个势垒。然而，量子力学允许一个低概率的事件发生，即 \(\alpha\) 粒子通过这个看似不可逾越的势垒“隧道”。

在量子隧道效应中，粒子有一定的概率出现在势垒的另一侧，即使它们的能量低于势垒的高度。这是因为量子力学中的粒子不仅具有粒子性，也具有波动性。\(\alpha\) 粒子在原子核内可以被描述为一个波函数，这个波函数在势垒内衰减，但不会完全消失。因此，有一个非零的概率，\(\alpha\) 粒子的波函数会延伸到势垒的另一侧，使得 \(\alpha\) 粒子能够“隧道”穿过势垒并逃逸。

这个隧道效应的概率非常小，这就是为什么 \(\alpha\) 衰变通常具有很长的半衰期。原子核的大小、\(\alpha\) 粒子的能量，以及势垒的高度和宽度都会影响这个概率。但一旦 \(\alpha\) 粒子隧道穿过势垒，它就能够逃逸出核并导致原子核衰变，从而产生一个新的元素。

隧道二级管

“隧道二极管”是一种半导体电子器件。这种二极管的特殊之处在于它利用量子隧道效应来实现其独特的电流-电压（ \(\rm I-V\) ）特性。在隧道二极管中，当两个半导体材料（一个是 N 型半导体，另一个是 P 型半导体）紧密接触时，它们之间形成一个非常薄的势垒。

在某些条件下，电子可以通过量子隧道效应穿过这个势垒，即使在常规条件下势垒似乎是不可逾越的。

图片链接

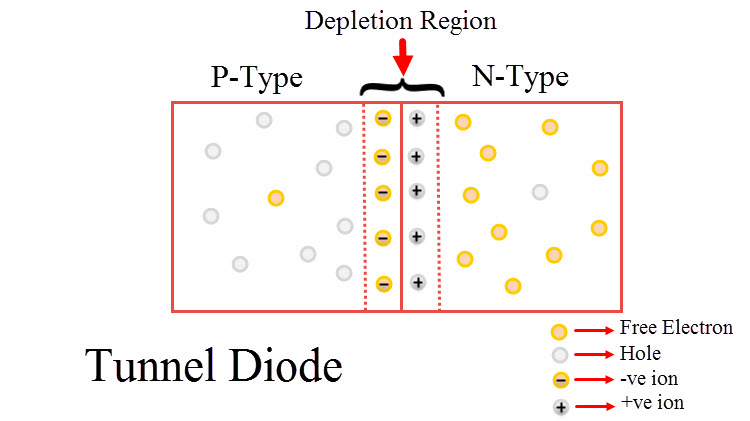
比如当施加适当的电压时，电子可以通过量子隧道效应穿越这个 PN 结构。

图片链接

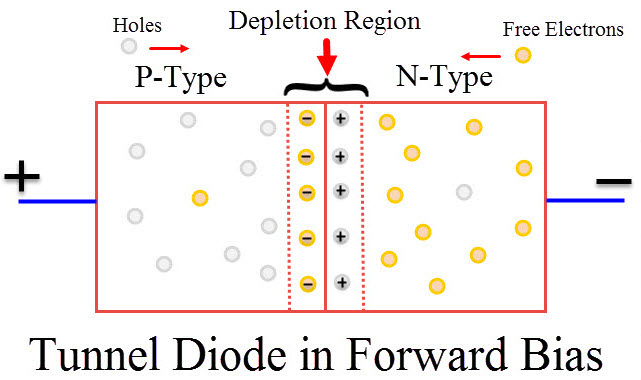
在隧道二极管中，当对它施加正向电压时，P 型材料的空穴和 N 型材料的电子在能带上相对位置变化，使得能带部分重叠。在这种情况下，电子可以通过量子隧穿从 N 型材料的导带跃迁到 P 型材料的价带。这种跃迁在经典物理学中是不可能的，因为电子必须穿越一个能量势垒，而这个势垒在量子力学中可以通过隧穿来克服。

图片链接

在隧道二极管中，电流随着电压增大的变化表现出几个独特的阶段，这些阶段直接反映了量子隧道效应的特性：

图片链接

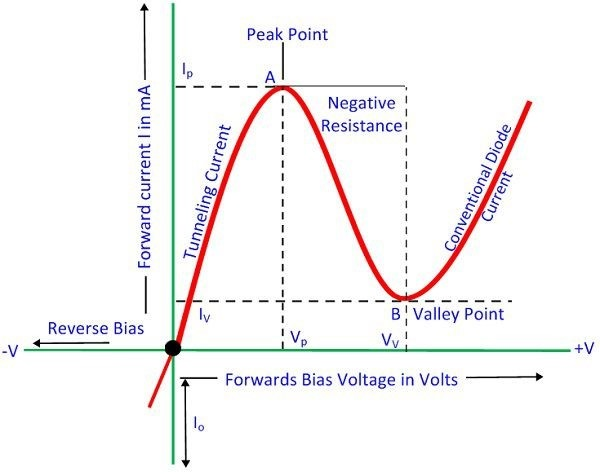
1. 初始增加阶段：当隧道二极管接收到低电压时，电子开始通过量子隧道效应从 N 型材料的导带隧穿到 P 型材料的价带。这时，随着电压的逐渐增加，电流也随之增加。这是因为势垒宽度减小，使得电子更容易隧穿过去。
2. 峰值电流阶段：当电压增加到特定水平时，电流达到峰值。在这一点上，电子隧穿的条件是最理想的，导致通过隧道二极管的电流达到最大值。
3. 负阻抗阶段：随着电压继续增加，超过峰值电流点后，电流意外地开始下降，即使电压还在增加。这个现象称为负阻抗。在这个阶段，由于能带对齐方式的改变，有效隧道势垒升高，使得电子难以隧穿，从而导致电流减少。
4. 饱和或正常二极管行为阶段：当电压继续升高，达到更高水平时，隧道二极管的行为开始转变，类似于普通二极管。在这个阶段，电流再次随着电压的增加而增加，但这不是由于量子隧道效应，而是因为普通的载流子注入机制开始占主导地位。

总之，隧道二极管利用量子隧道效应允许电子在没有足够能量越过势垒的情况下从一个半导体材料跃迁到另一个半导体材料，从而产生电流。

场离子显微镜（FIM）

图片链接

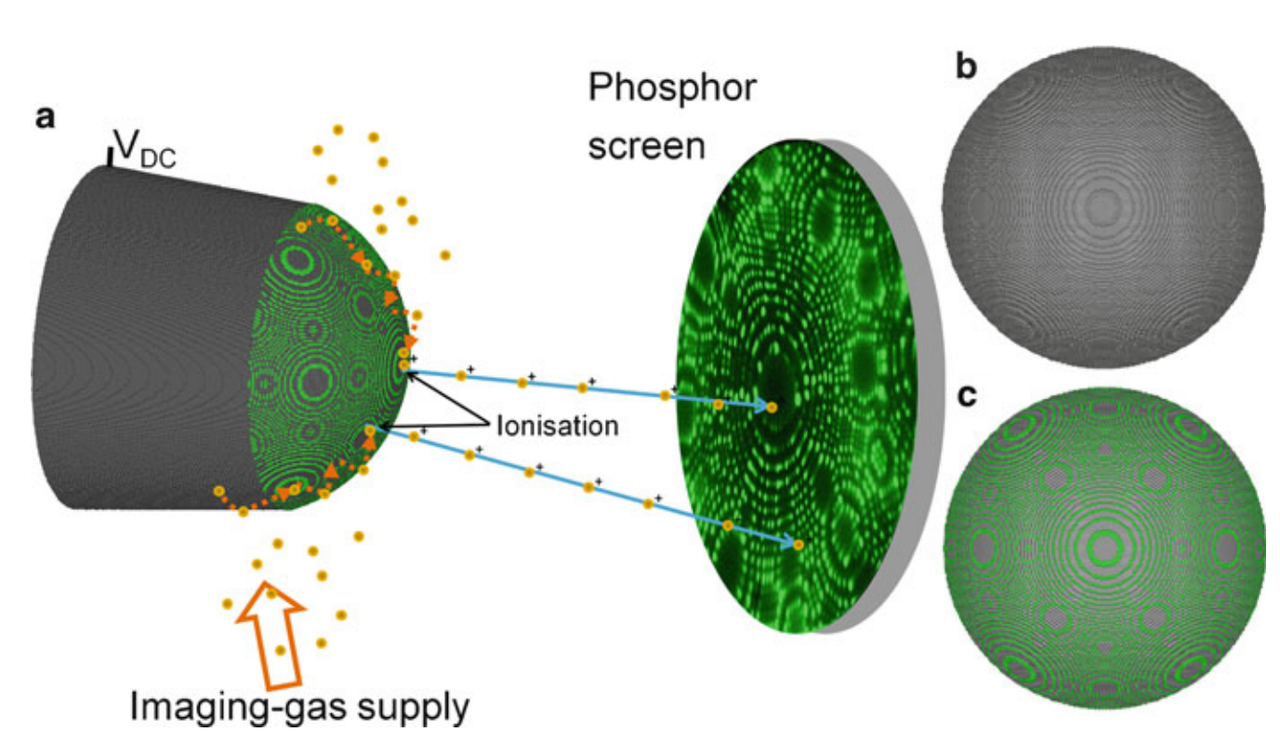
场离子显微镜（Field Ion Microscopy）是一种显微镜技术，用于观察金属和合金的原子结构。这种技术是在 20 世纪 50 年代由德国物理学家埃 Erwin Wilhelm Müller 发明的。场离子显微镜的工作原理是利用一个尖锐的样品尖端（通常是金属），在其表面创建一个非常高的电场。

Erwin Wilhelm Müller

图片链接

当将样品置于高电场中时，尖端附近的原子会被电离（因为量子隧道效应失去或获得电子），形成离子。这些离子会被加速并射向对面的荧光屏，形成样品表面原子的放大影像。由于原子被单独解析，所以场离子显微镜可以提供非常高的分辨率，理论上可以达到原子级别。

场离子显微镜主要用于材料科学、表面科学和纳米技术领域，尤其是在研究金属表面结构和表面化学反应的机制方面。但是，它也有一些限制，比如样品必须是电导性的，且必须能承受高电场和真空环境。此外，由于它基于场离子化的原理，因此主要适用于某些类型的材料，如金属。

扫描隧道显微镜（STM）

扫描隧道显微镜（STM，Scanning Tunneling Microscope）是由 Gerd Binnig 和 Heinrich Rohrer 在 1981 年发明的一种用于观察材料表面至原子级别的精细结构的仪器。这项技术的核心是量子隧穿效应，它基于的原理是即使两个导体间存在障碍物，电子也能从一个导体“隧穿”到另一个导体。

左：Gerd Binnig；右：Heinrich Rohrer

图片链接

STM 的发明极大地推动了纳米技术和表面科学的发展，使科学家能够首次直接观察到单个原子的表面结构。这种精细的观察能力对材料科学、物理学和化学等领域产生了深远的影响。因其在设计和构建扫描隧道显微镜方面的开创性工作，以及这项技术对科学的巨大贡献，Gerd Binnig 和 Heinrich Rohrer 共同获得了 1986 年诺贝尔物理学奖。

图片链接

STM 的主要组成部分包括：

1. 尖锐的探针：探针非常尖锐，通常只有一个原子的尖端。它被置于距样品表面几埃的距离（1 埃等于 0.1 纳米）。
2. 精确的定位机构：用于调整探针与样品表面之间的距离，以保持恒定的隧穿电流。
3. 反馈系统：根据隧穿电流的变化自动调节探针和样品之间的距离。

当探针靠近样品表面时，由于量子隧穿效应，即使它们之间没有实际接触，也会有微小的电流流过探针和样品之间的隙缝。探针沿样品表面扫描，同时记录通过隙缝的隧穿电流的变化。这些数据可以用来生成样品表面的三维图像，达到原子级别的分辨率。

评论